
[해당 포스팅은 "[기초개념] Graph Convolutional Network(GCN)"(GIST 발표자료) 를 참조했습니다. 링크: https://www.slideshare.net/slideshow/graph-convolutional-network-gcn/144158888#6 ]
1. 그래프 기본개념
- 그래프는 일반적으로 G = (V, E)로 정의되며 여기서 V는 노드의 집합을, E는 엣지의 집합을 의미합니다.
* 노드(Node) : 각각의 노드는 속성 벡터(feature)를 가지게 됩니다. 예를 들어, SNS 그래프에서 한 노드는 사용자에 해당하며 사용자의 속성(나이, 관심사 등)이 포함된 벡터가 그 노드의 특징 벡터입니다.
* 엣지(Edge) : 엣지는 노드 간의 연결을 나타내며, 엣지가 존재하면 노드들 간에 직접적인 관계아 있음을 의미합니다.
* 노드와 엣지의 예시
SNS에서 다음과 같은 데이터를 가정해봅니다. 이때, 노드는 사용자를 나타내며, 엣지는 사용자가 친구인지 여부입니다. 그리고, 노드에 대한 특징벡터(Feature vector)는 각 사용자의 나이, 관심사, 위치와 같은 정보를 의미한다고 해보겠습니다.
각 사용자는 Alice, Bob, Charlie, David이고 각 이름 앞 글자를 따서 노드를 만들고 (ex. Alice ==> Node "A"), 엣지는 각 사용자 간의 친구여부를 나타내며 아래와 같은 친구 관계를 가집니다.
.

( A와 B / B와 C / A와 D / B와 D 는 친구)
이를 행렬로 만든 것을 Adjacency Matrix라고 합니다.
| A | B | C | D | |
| A | 0 | 1 | 0 | 1 |
| B | 1 | 0 | 1 | 1 |
| C | 0 | 1 | 0 | 0 |
| D | 1 | 1 | 0 | 0 |
또한 각 노드의 특징을 정리하면 아래와 같다고 가정해보겠습니다.

이를 특징 벡터로 표현해보면
A : [25, 음악, 여행, 뉴욕]
B: [30, 스포츠, 영화, 샌프란시스코]
C: [35, 요리, 독서, 시카고]
D: [28, 사진, 음악, 보스턴] 으로 나타낼수 있고, 연산을 위해 범주형 변수를 숫자로 임베딩하면
(관심사 : 음악 = 1, 여행 = 2, 스포츠 = 3 , 영화 = 4, 요리 = 5, 독서 = 6, 사진 = 7)
(위치 : 뉴욕 = 1 , 샌프란시스코 = 2, 시카고 = 3, 보스턴 = 4)
A = [25 , 1 , 2, 1]
B = [30, 3, 4, 2]
C = [35, 5, 6, 3]
D = [28, 7, 1, 4]
라고 할 수 있습니다.
이를 행렬의 형태로 표현한 것을 Feature Matrix라 하며, 아래와 같이 표현할 수 있습니다.
| Feature1 | Feature2 | Feature3 | Feature4 | |
| A | 25 | 1 | 2 | 1 |
| B | 30 | 3 | 4 | 2 |
| C | 35 | 5 | 6 | 3 |
| D | 28 | 7 | 1 | 4 |
2. GCN (Graph Conovlutional Network)
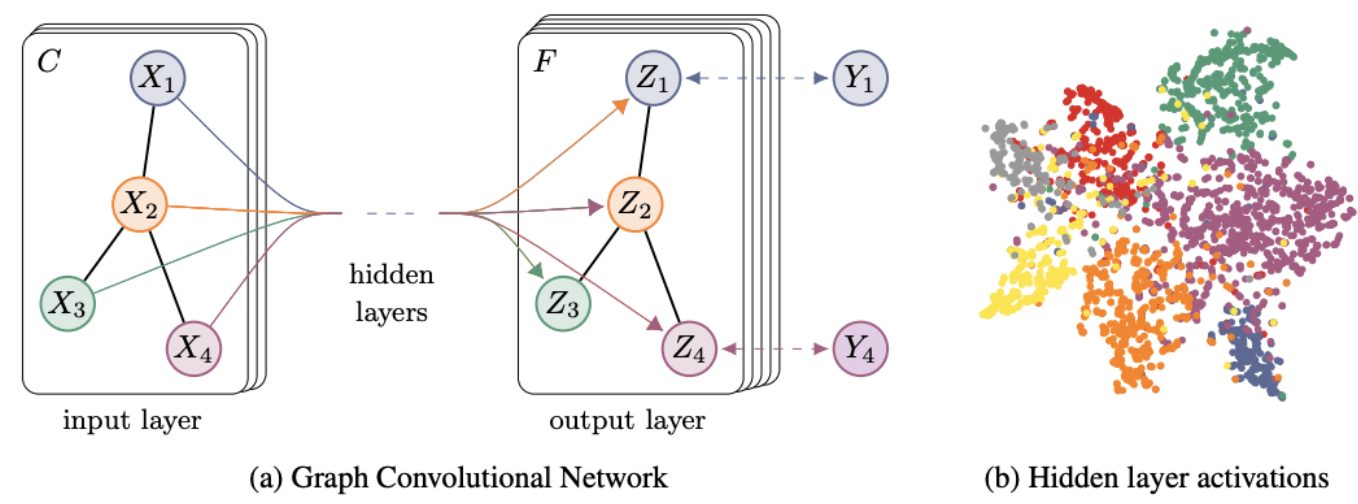
1) GCN의 핵심 아이디어는 노드의 표현을 이웃 노드의 정보와 합성하여 업데이트하는 것을 말합니다.
이를 통해 각 노드는 자신과 연결된 이웃 노드들의 정보를 수용하고 그 정보를 바탕으로 자신의 표현을 점진적으로 갱신하게 됩니다.
* 이미지에서 CNN을 활용 시 주변의 픽셀들의 정보를 활용하여 고차원의 벡터로 표현하듯, GCN도 이웃 노드들의 정보들을 활용해서 자신의 정보를 업데이트하는 방식이라고 보시면 되겠습니다.
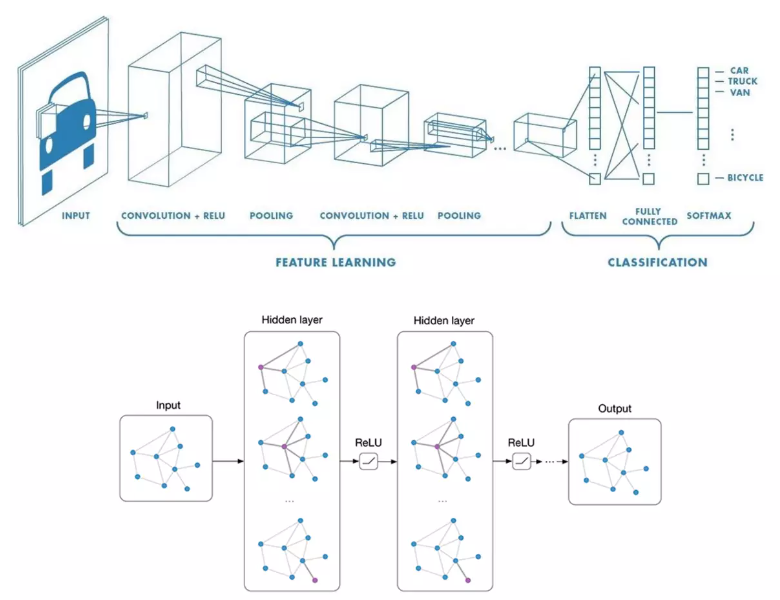
위 그림에서 Hidden layer에 보라색으로 표현된 부분이 업데이트 되는 노드이고, 그 노드를 업데이트 시키기 위해서는 해당 노드의 이웃 노드(neighbor node)를 활용하는 것이라고 보면 되겠습니다.
이때, 각 노드는 이웃 노드로부터 메시지를 받아들이고 이를 기반으로 자신의 표현을 갱신하는 것을 Message Passing이라고 합니다. 이 정보를 받아들이는 과정은, 각 이웃들로부터 받은 메시지(정보)를 가중합(Weighted Sum)하는 형태로 처리됩니다.
예를 들어 아래 그림과 같이 4개의 노드가 있고 각 노드는 5개의 Features를 가지고 있으며, Feature 별 크기를 Heatmap의 형식으로 표현하고 노드의 연결성을 Adjacency Matrix로 표현하면 아래 그림과 같습니다.
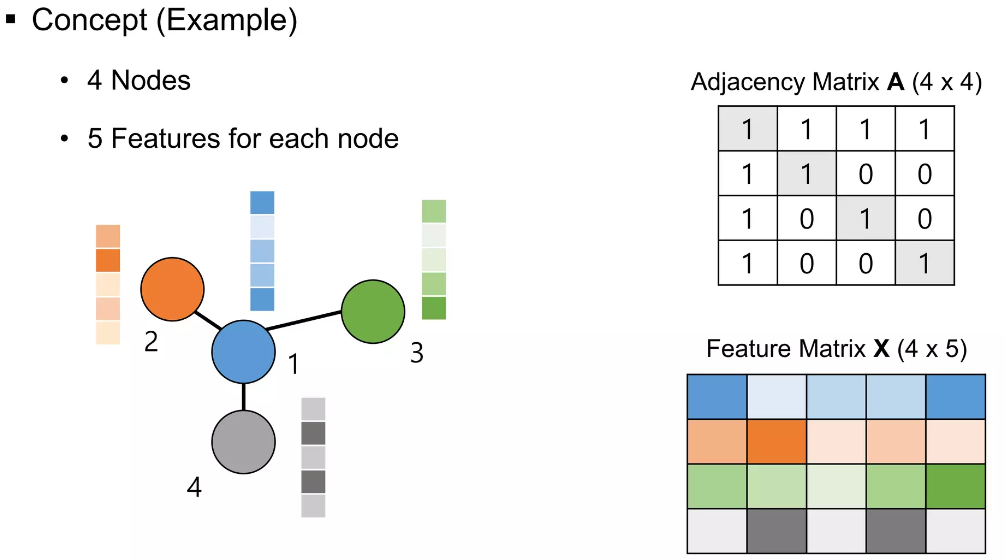
먼저, 1번 노드의 feature 값에 대해서 업데이트 하는 방법에 대해 알아보겠습니다.
1번 노드의 feature 값을 주변 노드 feature들의 가중합으로 업데이트 하는 것은 아래 그림과 같습니다.
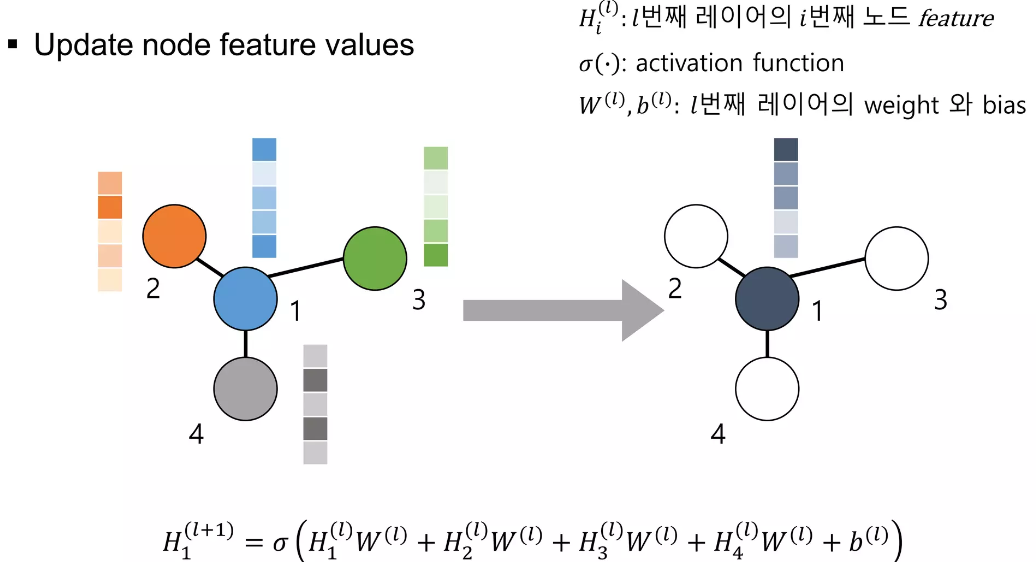
또한, 이때 곱해지는 가중치는 각 노드별 feature에 곱해질때 동일하게 공유됩니다.(Weight Sharing)
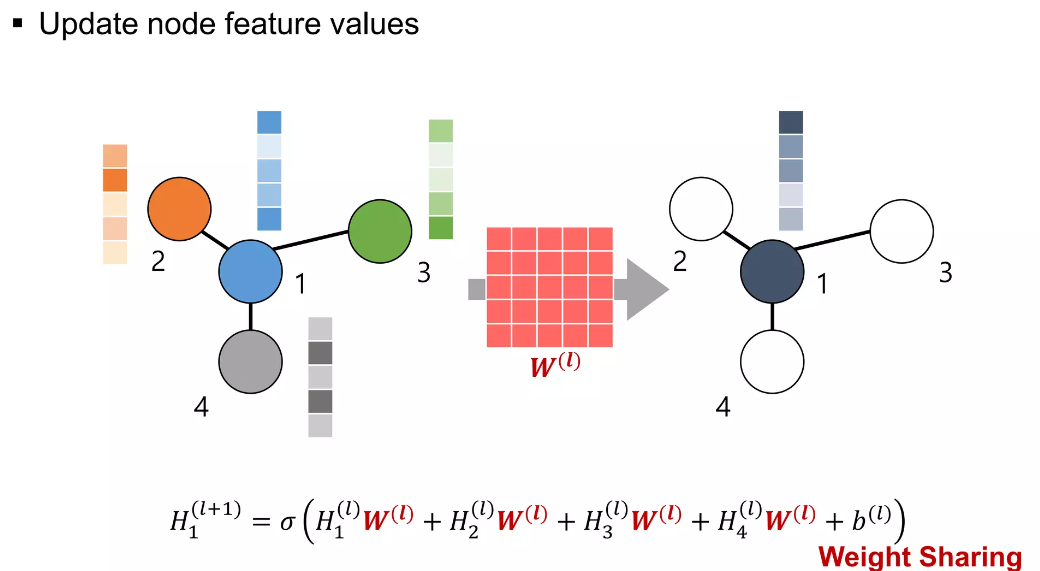
이와 같은 가중합으로 1번 노드의 값은 업데이트가 되고
2번 노드의 feature 업데이트의 경우에도 동일하게 일어나지만, 이번에는 2번이 1번하고만 연결되어 있기에 3번과 4번의 feature 행렬은 0으로 처리되어 해당 값들은 영향을 미치지 않게 됩니다.
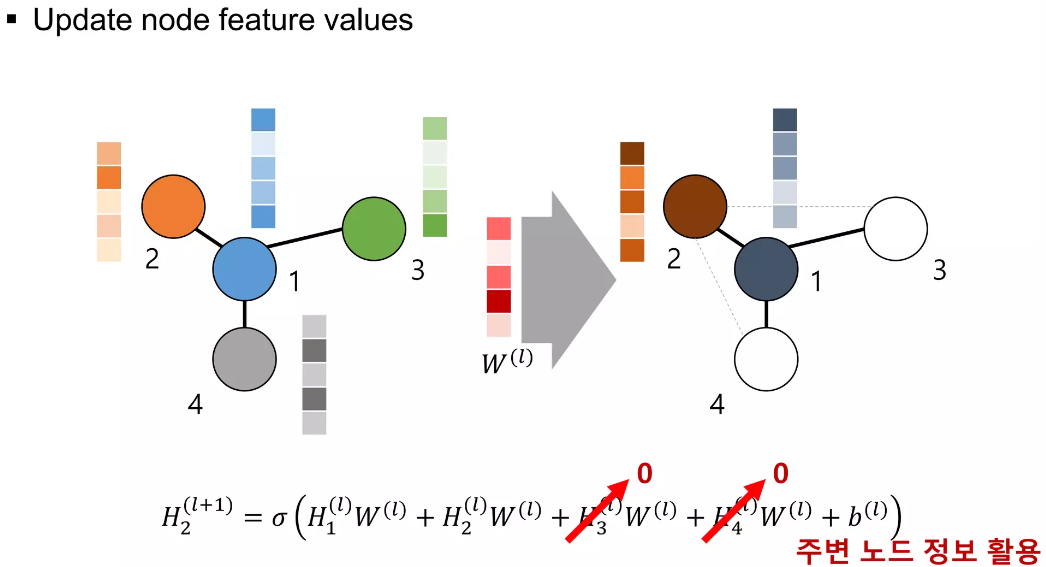
이와 같은 방식으로 3번과 4번의 노드가 업데이트가 되게 됩니다.
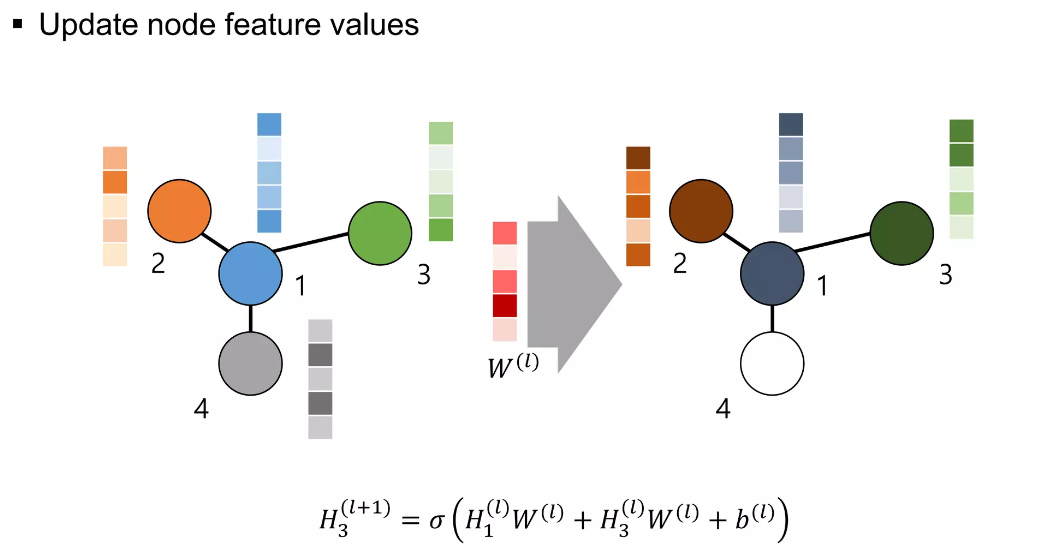
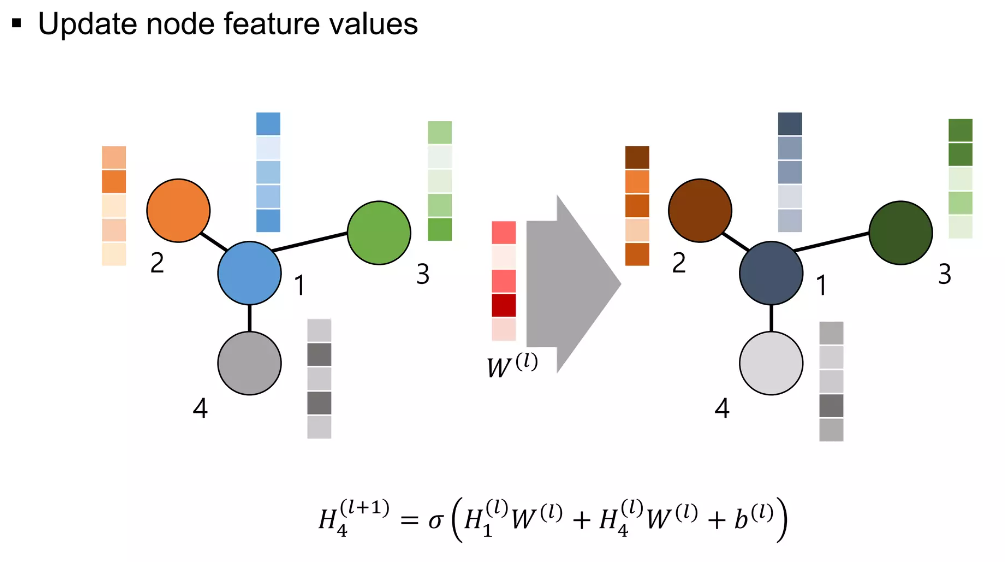
위와 같이 순차적인 계산을 통해, 각 노드들의 features도 순차적으로 업데이트가 되게 됩니다.
이와 같이 모든 노드의 features가 업데이트 되는 과정을 1개의 Neural Network의 Layer로 표현되고, 각 레이어의 별로 업데이트 되는 모습을 그림으로 표현하면 아래와 같습니다.
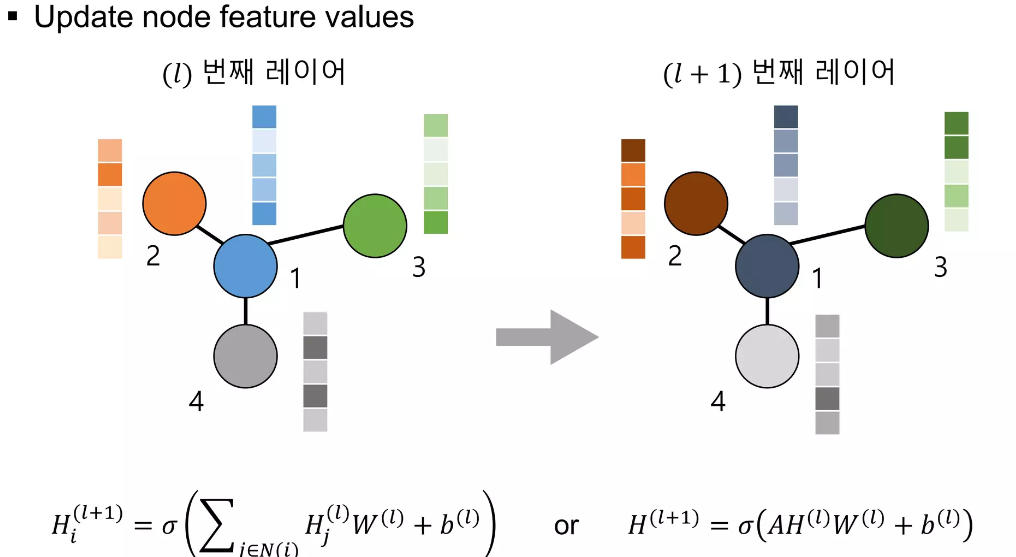
즉 이와 같은 구조가 다양한 Layer를 통해서 이루어지게 됩니다.
이때 위에서 보여주는 Weight와 Bias의 합은 이해를 위해 표현된 단순한 형태이며 실제 활용되는 수식은 아래와 같습니다.
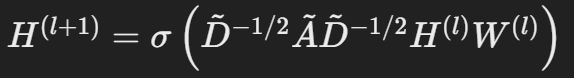

이 개념에 대해서 조금 더 알아보면,
* 수정된 인접행렬을 추가해 자기 자신과의 연결성을 위해 Adjacency Matrix에 Identity Matrix를 더한 것이고
* D와 D^(-1/2)는 정규화를 통해 네트워크가 깊어질수록 발생하는 gradient exploding 문제를 방지하기 위함입니다. 수정된 인접 행렬은 각 노드의 자기 자신과의 연결성을 반영하기 위해 Adjacency Matrix에 Identity Matrix를 더한 것입니다. 이는 자기 연결(Self-loop)을 추가하여, 각 노드가 자신의 정보를 유지하면서도 이웃 노드의 정보와 결합할 수 있도록 돕습니다.
2) Read out
위와 같이 모든 Node의 정보를 업데이트하는 과정을, 각 Node의 feature 벡터와 이웃 노드로부터의 정보를 학습 가능한 가중치(weight matrix)를 사용하여 결합하는 방식으로 수행합니다. 이 Matrix는 그래프 내 모든 Node의 feature에 대한 representation을 학습합니다.
CNN에서 이미지의 다양한 feature map을 통해 복잡한 패턴을 추출하는 것처럼, GCN도 다양한 Node의 representations을 도출함으로써 더 복잡하고 유의미한 패턴을 학습할 수 있습니다.
그리고 이렇게 도출된 다양한 feature representation을 특정 목적에 맞게 통합하는 과정이 필요할 때, 이 통합 과정을 Readout이라고 부릅니다.
아래 그림과 같이 5개의 features를 가진 4개의 노드들이 다양한 representations (Matrix 들)을 가지고 있을텐데, 이걸 각 노드별로 통합하는 것입니다. 이 통합을 위한 대표적인 방법으로는 Node-wise summation이 있겠습니다.
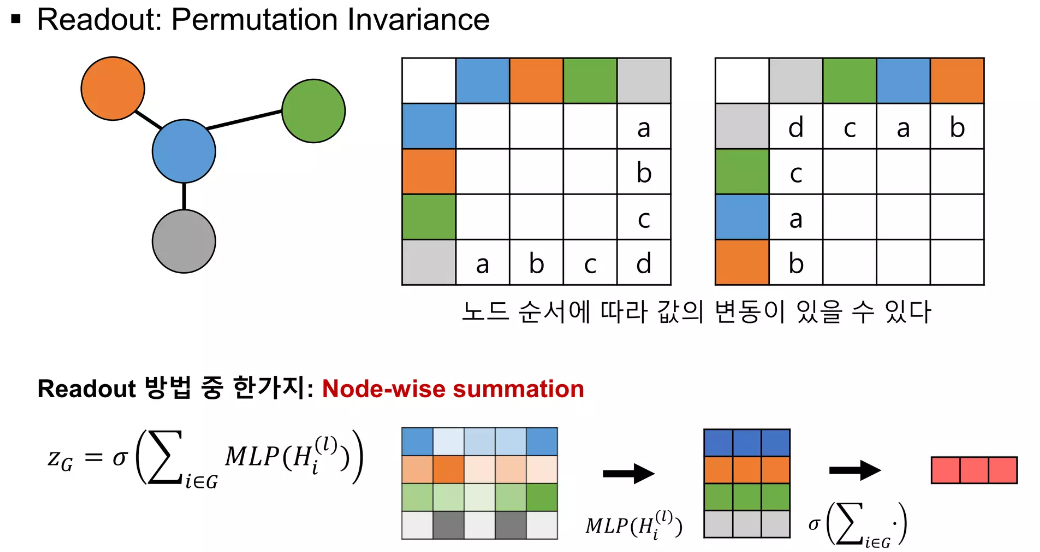
이와 같이 노드들에 대한 다양한 represnetaitons들(feature matrix)들을 통합하고, 이 노드들을 특정 Donw stream Task에 활용하면 되겠습니다.
아래 예시는 1개의 값을 예측(Regression 또는 Classification 등)을 위한 GCN의 전반적인 구조를 나타냅니다.
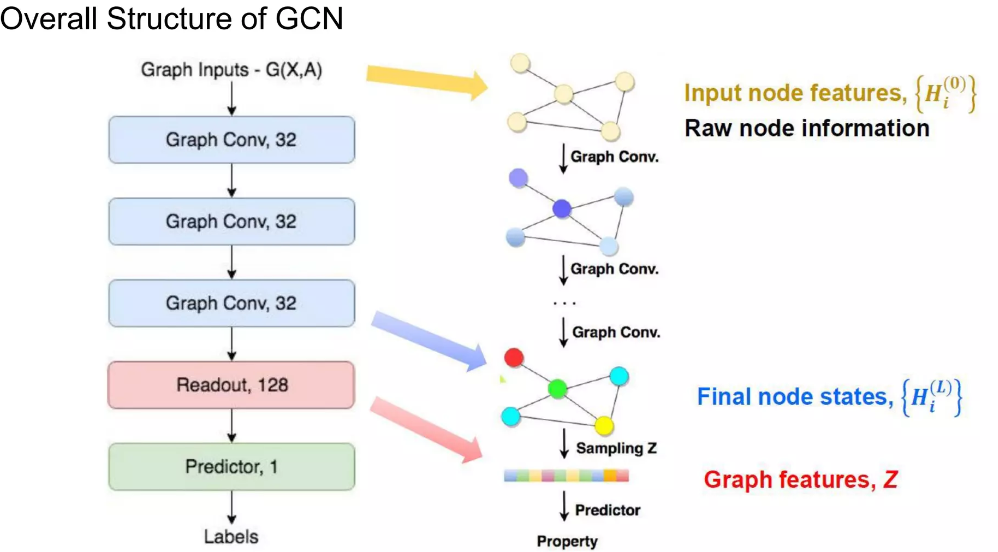
'딥러닝 with Python' 카테고리의 다른 글
| [개념정리] SiLU(Sigmoid Linear Unit) 활성화 함수 (1) | 2024.10.12 |
|---|---|
| [개념정리] Graph SAGE란? Graph SAmple & aggreGatE) (0) | 2024.09.29 |
| [개념정리] 그래프 신경망(Graph Neural Network / GNN) (3) (0) | 2024.08.02 |
| [개념정리] 그래프 신경망(Graph Neural Network / GNN) (2) (0) | 2024.08.01 |
| [개념정리] 그래프 신경망(Graph Neural Network / GNN) (1) (0) | 2024.07.31 |




댓글