
이번에 알아볼 것은 MLE(Maximum Likelihood Estimation)과 MAP(Maximum A Posteriori Estimaiton) 입니다.
1. MLE (최대우도추정)
- MLE는 주어진 데이터가 가장 설명될 수 있는 파라미터 값을 선택하는 것을 말하며, 이때 우도 함수(Likelihood Function)을 최대화하는 파라미터 값을 찾는 것을 말합니다.
- MLE는 아래와 같이 3단계로 나누어서 진행됩니다.
1) 우도 함수 정의

2) 로그 우도 함수
* 계산을 간소화하기 위해 우도 함수의 로그를 취한 로그 우도함수가 자주 사용됩니다.
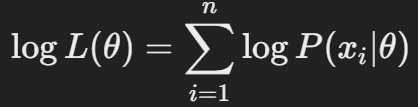
3) 로그 우도 함수 최대화
* 로그 우도 함수를 최대화하는 파라미터인 theta를 찾습니다.

* 보통 로그 우도 함수의 파라미터인 theta에 대한 도함수를 구하고 이를 0으로 하는 theta를 찾는 것입니다.
- 예시 : 정규분포

2. MAP(최대사후확률추정)
- MAP는 사전 지식이나 신념을 통합하여 통계 모델의 파라미터를 추정하는 방법을 말합니다. 이는 사후 확률(Posterior Distribution)을 최대화하는 파라미터 값을 선택하는 것입니다.
- MAP의 단계는 다음과 같이 4단계로 나뉘어집니다.
1) 사전 분포 정의
* 사전 분포 P(theta)는 데이터를 관찰하기 전에 파라미터 theta에 대한 사전 신념을 의미합니다.
2) 사후 분포 정의
* 베이즈 정리를 사용해 사후 분포를 다음과 같이 정의합니다.

3) 로그 사후 함수
* 로그를 취한 사후 함수는 다음과 같습니다.

4) 로그 사후 함수 최대화

-예시 :

3. MLE와 MAP의 비교
1) 목적
* MLE는 우도만 최대화하는 것을 목표로 함
* MAP는 사전 신념을 사전 분포를 통해 통합
2) 사용시기
* MLE : 사전 정보가 없거나 오직 관찰된 데이터에 의존하고자 할 때
* MAP : 사전 정보가 있고 이를 고려해야할 때
3) 계산 복잡성
* MLE와 MAP는 유사한 계산 복잡성을 가질 수 있지만, 사전 분포가 복잡한 경우 MAP는 더 복잡할 수 있음
4) 결과
* MLE는 특히 샘플 크기가 작을 때 데이터에 더 민감
* MAP는 데이터와 사전 지식을 결합하여 더 균형 잡힌 추정을 제공
** MLE와 MAP 모두 데이터가 많다면 두 결과는 크게 다르지 않을 것이나, 데이터가 적다면 사전 지식을 활용한 MAP가 더 유용한 결과를 도출해낼 수 있음
'딥러닝 with Python' 카테고리의 다른 글
| [개념 정리] N-gram이란? N-gram 언어 모델이란? (0) | 2024.07.27 |
|---|---|
| [개념 정리] 형태소 분석(Morphological Analysis) (0) | 2024.07.26 |
| [딥러닝 with Python] Multiple Instance Learning을 활용한 이미지 분류[개념 정리] (0) | 2024.07.23 |
| [딥러닝 with Python] Vision Transformer를 활용한 이미지 분류 (2) | 2024.07.23 |
| [딥러닝 with Python] KL Divergence Loss란? (2) | 2024.07.22 |




댓글