
[본 포스팅은 "Must Have 텐초의 파이토치 딥러닝 특강"의 내용을 참조하여 작성하였습니다]
텐서플로에서 파이토치로 넘어가기 위해 입문서로 시작했던 책이 위 책의 내용을 기반으로 파이토치에 대해 공부한 내용들을 정리해보고자 합니다.
첫 번째로는 파이토치를 통해서 사인함수를 만드는 것입니다.
사인함수를 만드는 방법은 1) 임의의 다항식 만들기, 2) 다항식의 계수들을 파이토치로 작성한 딥러닝 코드로 업데이트 하여 사인함수에 근사한 함수를 만드는 것입니다.
1. 파이토치로 사인함수 만들기
1) 먼저 필요한 라이브러리를 불러와줍니다. 이때는 math와 torch, 그리고 시각화를 위해 pyplot을 불러오겠습니다.
|
1
2
3
|
import math
import torch
import matplotlib.pyplot as plt
|
cs |
2) torch의 linspace 기능을 활용해서 등간격의 일련의 숫자를 만들어줍니다.
이때, 범위는 원주율인 pi (3.141592..)를 활용해 (-pi, pi) = (-3.141592, 3.141592)로 정해주고, 그 사이에 등 간격의 1,000개의 숫자를 만들어 x로 저장합니다.
저장된 x의 첫번째 10개는 아래와 같습니다.
|
1
2
|
x = torch.linspace(-math.pi, math.pi, 1000)
x[1:10]
|
cs |

3) 생성된 각 x값들을 torch.sin()함수를 활용해 사인함수에 입력값으로 넣은 것을 y로 정의합니다.
생성된 y의 첫번째 10개는 아래와 같습니다.
|
1
2
|
y = torch.sin(x)
y[1:10]
|
cs |

4) 다음은 임의의 랜덤숫자를 만듭니다. 각 a,b,c,d로 명하고, 그 결과는 아래와 같습니다.
|
1
2
3
4
5
6
|
a = torch.randn(())
b = torch.randn(())
c = torch.randn(())
d = torch.randn(())
a,b,c,d
|
cs |

5) 위에서 생성된 a,b,c,d를 계수 및 절편으로, 그리고 x 값들을 각 3차식, 2차식, 1차식에 넣어서 계산된 값을 y_random으로 정의하고 그 값 10개를 출력해봅니다.
|
1
2
|
y_random = a * x**3 + b * x**2 + c * x + d
y_random[1:10]
|
cs |

6) 우선 학습 전에 sine함수와 위 다항식을 비교해보겠습니다.
두 함수모두 범위는 -pi ~ pi 이며, 위에서 생성된 x를 a) sine함수에 넣은 결과, b) y_random 이라는 다항식에 넣은 결과를 시각화 하면 아래와 같습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
# 실제 y값으로 사인곡선 만들기
plt.subplot(2, 1, 1)
plt.title("y true")
plt.plot(x, y)
# 임의의 가중치로 만든 예측용 y값으로 사인곡선 만들기
plt.subplot(2, 1, 2)
plt.title("y radnom")
plt.plot(x, y_random)
# 그래프 출력하기
plt.show()
|
cs |
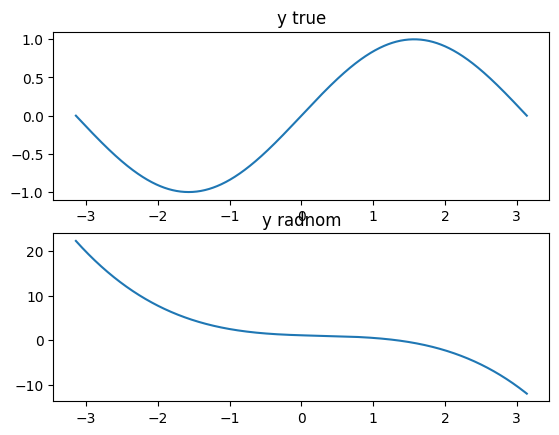
7) 이번에는 위에서 만들어진 다항식의 계수(a,b,c,d)를 업데이트하여 sine함수와 유사한 결과값이 나오도록 해보겠습니다.
방법은 다음과 같습니다.
a) 먼저, 실제 sine 함수의 값(y) 와 다항식의 값(y_random)의 차이의 제곱을 loss로 정의합니다.
b) 다음은 각 다항식의 계수, 기울기에 대한 미분값을 구해줍니다.
* y_pred(y의 예측값)의 경우, Loss = (y_pred - y)**2 으로 정의된 것에서 y_pred에 대해 미분한 값인 2(y_pred-y)이 나오고
* a의 경우, Loss(위와 동일)에서 a에 대해 편미분을 하고, loss가 모든 x에 대해 정의된 y에 대한 식이므로 전체를 더해준다. b,c,d,도 동일
c) 구해진 미분값에 learning rate을 곱해서 빼주는 경사하강법을 통해 각 a,b,c,d로 정의된 가중치들을 업데이트 해줍니다.
ex) a는 a - learning rate * grad_a 로 업데이트 됩니다.
d) 이와 같은 과정을 계속 반복하면서 오차( y 와 y_pred의 제곱의 차이)를 줄여갑니다.
이번 예제에서는 2000번동안 위 과정을 반복합니다. 그리고 그 결과는 아래와 같습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
earning_rate = 1e-6 # 학습률 정의
for epoch in range(2000): # 학습 2000번 진행
y_pred = a * x**3 + b * x**2 + c * x + d
loss = (y_pred - y).pow(2).sum().item() # ❶ 손실 정의
if epoch % 100 == 0:
print(f"epoch{epoch+1} loss:{loss}")
grad_y_pred = 2.0 * (y_pred - y) # ❷ 기울기의 미분값
grad_a = (grad_y_pred * x ** 3).sum()
grad_b = (grad_y_pred * x ** 2).sum()
grad_c = (grad_y_pred * x).sum()
grad_d = grad_y_pred.sum()
a -= learning_rate * grad_a # ❸ 가중치 업데이트
b -= learning_rate * grad_b
c -= learning_rate * grad_c
d -= learning_rate * grad_d
plt.subplot(3, 1, 1)
plt.title("y true")
plt.plot(x, y)
plt.subplot(3, 1, 2)
plt.title("y pred")
plt.plot(x, y_pred)
plt.subplot(3, 1, 3)
plt.plot(y_random)
plt.title("y random")
plt.show()
|
cs |
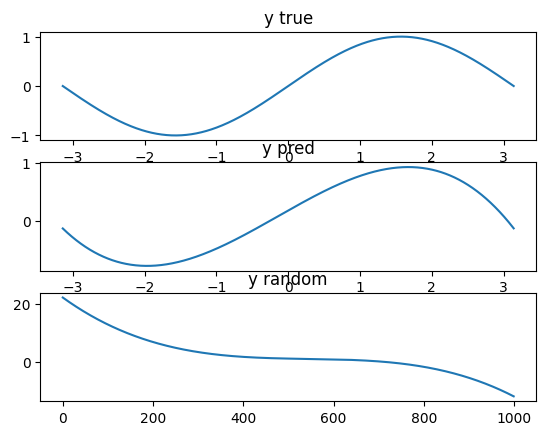
결과, 최초 y_random 이었던 y값은, 2,000번의 경사하강법 적용을 통해 y_pred가 되었고, 이는 sine함수에도 도출된 y_true와 꽤나 유사한 값을 가짐을 알 수 있습니다.
이번 포스팅에서는 pytorch의 torch 기능에 대해서 알아보았는데요.
이 torch기능은 numpy의 기능과 유사하며, 간단한 조작을 통해 서로 쉽게 변환이 가능합니다.
이러한 차이점 등으로 인해, tensor에 대한 표현이 달랐던 tensor flow 보다는 최근에 pytorch에 대한 인기가 높아지고 있는 것 같습니다.
'딥러닝 with Python' 카테고리의 다른 글
| [딥러닝 with 파이썬] PReLU란? Parametric ReLu란? (활성화함수, Activation Function) (0) | 2023.10.03 |
|---|---|
| [딥러닝 with 파이썬] ResNet(잔차신경망)의 개념 (2/2) / CIFAR-10 활용해서 이미지 분류모델 구현 (0) | 2023.10.01 |
| [딥러닝 with 파이썬] RESNET(잔차신경망)의 개념 (1/2) (1) | 2023.10.01 |
| [딥러닝 with 파이썬] 분류(Classification) / MNIST 데이터 사용 (0) | 2023.09.29 |
| [딥러닝 with 파이썬] 코랩에서 한국어용 Mecab 설치하기 (0) | 2023.09.20 |




댓글