[머신러닝 with Python] TPOT을 활용한 Iris 데이터 분류(AutoML)

 

이번에는 지난번에 알아본 여러 AutoML 라이브러리 중 TPOT을 활용해 Iris 데이터에 대한 분류를 진행해보고자 합니다.

 

1. TPOT이란?

- TPOT은 자동화된 머신러닝, 즉 AutoML의 도구로, 데이터를 전처리하고 최적의 머신러닝 모델과 하이퍼파라미터를 튜닝할 수 있는 라이브러리입니다. 

- 자세한 내용은 아래 포스팅을 참조하시면 되겠습니다.

[머신러닝 with Python] AutoML이란? (AutoML의 정의, 종류 등)

[머신러닝 with Python] AutoML이란? (AutoML의 정의, 종류 등)

 

2. TPOT을 활용한 Iris 데이터 분류 

Scikit learn 라이브러리에 내장되어있는 Iris 데이터를 활용해서 분류를 진행해보겠습니다.

[머신러닝 with 파이썬] PCA / 주성분 분석 / 차원축소 /iris 데이터 활용

[머신러닝 with 파이썬] PCA / 주성분 분석 / 차원축소 /iris 데이터 활용

 

Iris 데이터에 대한 설명은 위 포스팅을 참조하시면 되겠습니다.

 

먼저, 라이브러리를 설치해줍니다. tpot과 scikit-learn을 설치해줍니다.

pip install tpot scikit-learn

 

다음으로, TPOT을 활용해 분류작업을 진행해주겠습니다. 데이터는 Iris 데이터이고 사이킷런에 내장된 데이터를 활용해보겠습니다.

 

from tpot import TPOTClassifier

from sklearn.datasets import load_iris

from sklearn.model_selection import train_test_split

# 데이터 로드

iris = load_iris()

X, y = iris.data, iris.target

# 데이터 분리 (학습용과 테스트용)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# TPOT 분류기 정의

tpot = TPOTClassifier(generations=5, population_size=20, verbosity=2, random_state=42)

# 학습

tpot.fit(X_train, y_train)

# 정확도 출력

print("Test Accuracy: ", tpot.score(X_test, y_test))

# 최적의 파이프라인 코드 출력

tpot.export('tpot_optimized_pipeline.py')

 

유전 알고리즘을 바탕으로 하이퍼 파라미터를 최적화함을 알 수 있으며, 5번째 Generation까지 진행되었음에도 Best CV 스코어는 0.9833입니다.

 

결국 도출된 최적의 모델은 MultinomialNB(다항 나이브 베이즈)와 Logistic Regression의 조합입니다.

 

테스트 데이터에 대한 분류 결과는 100%가 나오게 되었습니다.

 

이때 활용된 MultinomialNB(다항 나이브 베이즈)는 주로 범주형 데이터를 처리하는데 적합한 방법으로, 데이터를 사전에 전처리할 때 MultionmialNB를 활용하였습니다.

 

이때 alpha=10인데 이는 라플라스 스무딩 파라미터 값ㅅ이고, 값이 클수록 확률 분포를 더 균등하게 만들어줍니다. 또한, fit_prior=False의 의미는 사전 확률을 학습 데이터로부터 추정하지 않도록 설정하는 것으로, 이는 데이터의 클래스 분포를 무시하고 고정된 사전확률을 활용한다는 것입니다.

 

다음으로, 분류기로 활용된 모델은 Logistic Regression으로 C=25의 의미는 규제 강도에 대한 역수를 의미하고 값이 작을수록 더 강한 규제를 의미하는데 25라는 꽤 큰 값이 선택되었기에 규제가 상당히 약함을 알 수 있습니다.

 

dual=False의 의미는 데이터가 작거나 희소하지 않을 경우 선형 Solver를 사용하도록 한다는 것이고, Penalty =l2는 L2 정규화를 사용해 모델의 가중치를 최소화하면서 과적합을 방지하기 위한 정규화 기법을 의미한다는 것입니다.

 

그렇다면 분류된 결과를 시각화 해보도록 하겠습니다. 

 

먼저 Confusion Matrix를 활용해 시각화 해보겠습니다.

from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay

# 예측 수행

y_pred = tpot.predict(X_test)

# 혼동 행렬 생성

cm = confusion_matrix(y_test, y_pred)

# 혼동 행렬 시각화

disp = ConfusionMatrixDisplay(confusion_matrix=cm, display_labels=iris.target_names)

disp.plot(cmap='Blues')

import matplotlib.pyplot as plt

plt.title("Confusion Matrix")

plt.show()

 

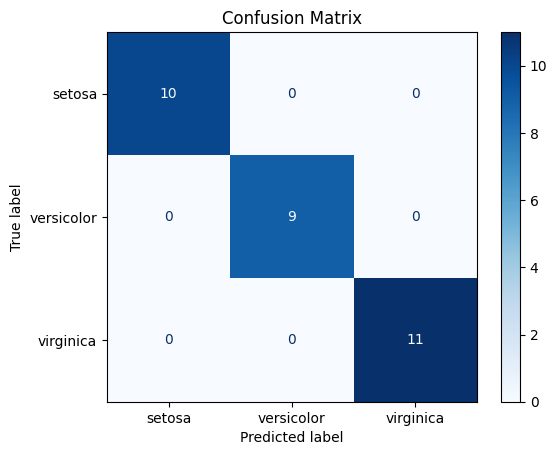
실제 레이블과 예측 레이블이 정확히 일치함을 알 수 있습니다.

 

 

다음은 ROC Curve입니다.

from sklearn.metrics import roc_curve, auc

import matplotlib.pyplot as plt

from sklearn.preprocessing import label_binarize

from sklearn.metrics import roc_auc_score

# 이진화된 레이블 (Multiclass ROC 지원)

y_test_bin = label_binarize(y_test, classes=[0, 1, 2])

y_pred_prob = tpot.predict_proba(X_test)

# 각 클래스에 대해 ROC Curve 계산

for i in range(y_test_bin.shape[1]):

    fpr, tpr, _ = roc_curve(y_test_bin[:, i], y_pred_prob[:, i])

    roc_auc = auc(fpr, tpr)

    plt.plot(fpr, tpr, label=f'Class {i} (AUC = {roc_auc:.2f})')

plt.plot([0, 1], [0, 1], 'k--')  # Random guess line

plt.xlabel('False Positive Rate')

plt.ylabel('True Positive Rate')

plt.title('ROC Curve')

plt.legend()

plt.show()

모든 클래스에 대해 1이라는 AUC Score가 도출되었습니다.

 

 

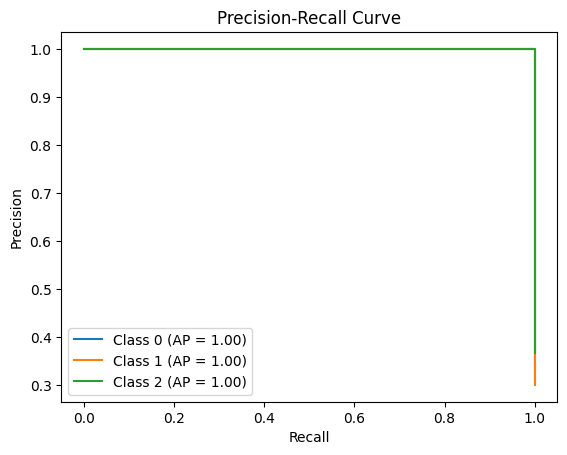
다음은 Precision-Recall Curve이고, 역시나 정확하게 잘 나옴을 알 수 있습니다.

from sklearn.metrics import precision_recall_curve, average_precision_score

# 각 클래스에 대해 Precision-Recall Curve 계산

for i in range(y_test_bin.shape[1]):

    precision, recall, _ = precision_recall_curve(y_test_bin[:, i], y_pred_prob[:, i])

    avg_precision = average_precision_score(y_test_bin[:, i], y_pred_prob[:, i])

    plt.plot(recall, precision, label=f'Class {i} (AP = {avg_precision:.2f})')

plt.xlabel('Recall')

plt.ylabel('Precision')

plt.title('Precision-Recall Curve')

plt.legend()

plt.show()