
생성 모델은 데이터를 학습하고 새로운 데이터를 생성하는 능력을 갖춘 기계 학습 모델입니다. 이 모델들은 종종 복잡한 데이터 분포를 단순한 분포로 변환하거나 반대로 단순한 분포에서 복잡한 데이터를 생성하는 과정에서 가우시안 분포(Gaussian Distribution)를 활용합니다. 그 이유는 무엇일까요?
이번 포스팅에서는 생성 모델의 주요 유형인 Variational Autoencoder(VAE), Normalizing Flow, Diffusion Models에서 가우시안 분포가 왜 중요한지에 대해 자세히 살펴보겠습니다.
[가우시안 분포 : 연속 확률 분포의 한 종류로 다음과 같은 확률 밀도 함수를 가지며, 평균과 분산을 통해 해당 데이터의 분포를 표현가능
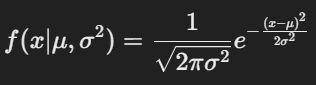
가우시안 분포의 특징
* 대칭성 : 분포는 평균을 중심으로 좌우 대칭
* 중심 극한 정리 : 독립적이고 동일한 분포를 따르는 많은 변수들의 합은 가우시안 분포에 근사
* 모멘트 : 평균, 분산, 왜도, 첨도 등의 모멘트가 존재함. 이때 왜도는 0, 첨도는 3임 ]
1. Variational Autoencoder(VAE)에서의 가우시안 분포 활용
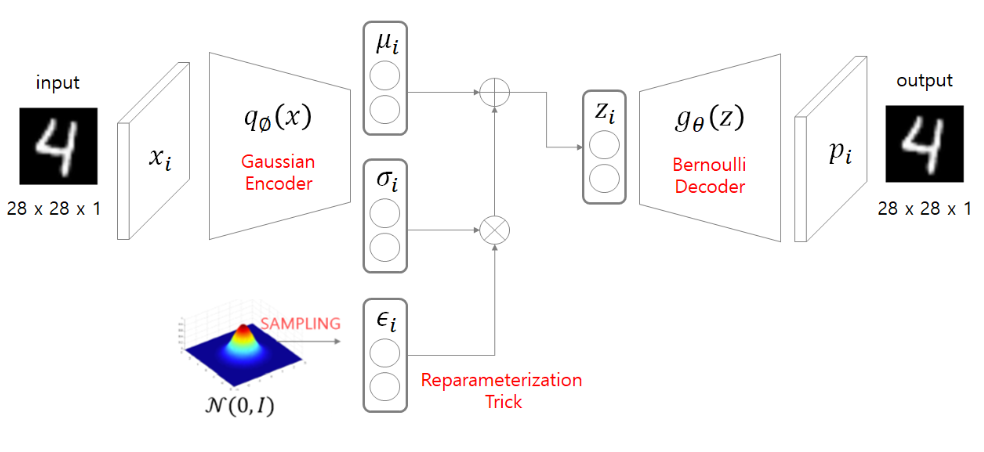
1) 잠재공간의 연속성
- VAE는 입력 데이터를 잠재 공간(latent space)으로 매핑한 후, 이 잠재 공간에서 샘플링하여 새로운 데이터를 생성합니다. 가우시안 분포를 사용하면 잠재 공간에서의 샘플링이 연속적이고 매끄럽게 이루어질 수 있습니다. 이는 새로운 데이터 포인트를 생성할 때 매우 유리합니다.
2) KL Divergence 계산의 용이성
- VAE는 입력 데이터의 잠재 분포와 가우시안 분포 사이의 차이를 최소화하기 위해 KL Divergence를 사용합니다. 가우시안 분포는 이 KL Divergence를 수학적으로 쉽게 계산할 수 있도록 합니다.
3) 수학적 단순성
- 가우시안 분포는 평균과 분산이라는 두 개의 매개변수만으로 완전히 정의될 수 있기 때문에 모델을 학습하고 최적화하는 과정이 단순해집니다.
2. Normalizing Flow에서의 가우시안 분포 활용

1) 베이스 분포
- Normalizing Flow는 복잡한 데이터 분포를 가우시안 분포와 같은 단순한 분포로 변환합니다. 가우시안 분포를 베이스 분포로 사용하면 모델의 출력 분포가 가우시안 분포를 따르도록 훈련할 수 있기에 변환 과정의 안정성을 보장해줍니다.
2) 가역성(Invertibility)과 미분가능성(Differentiability)
- 가우시안 분포는 수학적으로 다루기 쉬운 특성 덕분에 변환이 가역적(Invertible)이며 미분 가능(Differentiable)합니다. 이는 학습 과정에서 필수적입니다.
3. Diffusion Models에서의 가우시안 분포 활용
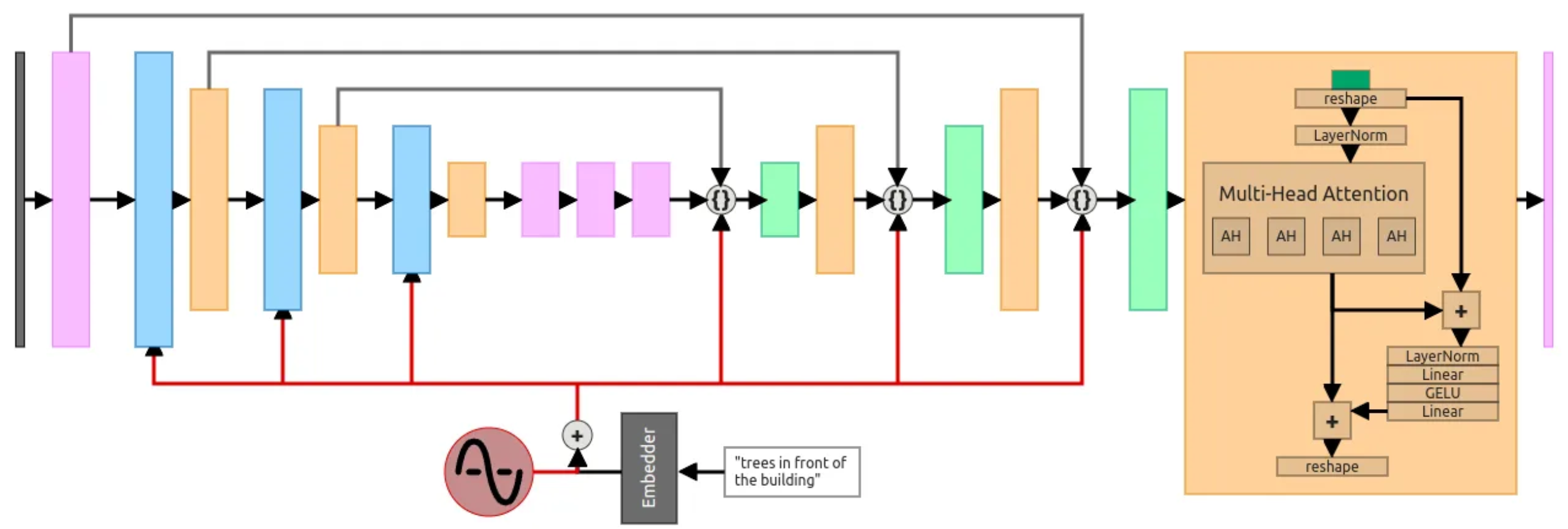
1) 노이즈 모델링
- Diffusion Models은 데이터에 점진적으로 노이즈를 추가하고 이를 다시 제거하는 과정을 통해 데이터를 생성합니다. 여기서 가우시안 노이즈는 데이터에 추가되는 노이즈로 자주 사용됩니다. 이는 가우시안 분포의 성질인 중심 극한 정리에 의해 실제 데이터에 노이즈를 추가할 때 자연스러운 결과를 보장합니다.
2) 정규화된 변환
- 가우시안 분포는 변환 과정에서 노이즈를 추가하거나 제거하는 계산을 단순화합니다. 이는 학습 및 생성 과정에서 매우 효율적입니다.
3) 수학적 특성
- 가우시안 분포의 특성상 노이즈를 제거하는 역과정(reverse process)도 안정적이고 수학적으로 다루기 쉽습니다.
이를 통해 가우시안 분포를 생성 모델에서 활용하는 이유를 정리해보면 다음과 같습니다.
1. 수학적 용이성 : 가우시안 분포는 수학적으로 잘 정의되고 있고 계산이 용이
2. 중심 극한 정리 : 많은 실제 데이터가 가우시안 분포에 가까운 성질을 가지며, 이는 모델링에 매우 유리
3. 최적화 효율성 : 많은 최적화 알고리즘이 가우시안 분포를 가정할 때 더욱 효과적으로 동작
4. 연속적 샘플링 : 연속적이고 매끄러운 데이터 생성이 가능
5. KL Divergence의 요이성 : VAE와 같은 모델에서 KL Divergence 계산이 용이하게 해줌
6. 노이즈 모델링의 자연 스러움 : Diffusion 모델에서 노이즈를 자연스럽게 추가 및 제거
'딥러닝 with Python' 카테고리의 다른 글
| [딥러닝 with Python] 이미지 분류(Image Classification) (1) | 2024.06.14 |
|---|---|
| [딥러닝 with Python] 노멀라이징 플로(Normalizing Flow) (0) | 2024.06.09 |
| [딥러닝 with Python] LSTM (Long Short Term Memory) (2) | 2024.06.06 |
| [딥러닝 개념정리] ProGAN (Progressive Growing of GANs) / PGAN (0) | 2024.06.05 |
| [딥러닝 with Python] 조건부 GAN / CGAN / Conditional GAN (0) | 2024.06.04 |




댓글