[본 포스팅은 "만들면서 배우는 생성 AI 2판" 을 참조했습니다]
이번에 알아볼 모형은 노멀라이징 플로(Normalizing Flow) 입니다.
노멀라이징 플로는 기존에 알아본 변이형 오토인코더(VAE)와 유사합니다.
변이형 오토 인코더에서는 인코더를 학습하여 복잡한 분포와 샘플링이 가능한 훨씬 간단한 분포 사이를 매핑하지였고, 그런 다음 디코더를 학습하여 단순한 분포에서 복잡한 분포로 매핑하는 과정을 거쳤습니다.
따라서 단순한 분포에서 포인트 z를 샘플링하여 학습된 변환을 적용하면 새로운 데이터 포인트를 생성할 수 있었습니다.
이 과정을 확률적으로 표현해보자면
디코더 : p(xㅣz) 인코더 : q(zㅣx) (디코더의 분포인 p()의 근사치인 q를 활용함)
과 같습니다. 즉, 인코더와 디코더는 서로 다른 두개의 신경망이라고 볼 수 있습니다.
[생성 AI] 변이형 오토인코더(Variational Auto Encoder) (1/2)
[생성 AI] 변이형 오토인코더(Variational Auto Encoder) (1/2)
[해당 포스팅은 "만들면서 배우는 생성 AI 2탄"을 참조했습니다] 1. 변이형 오토인코더(VAE, Variational Auto Encoder)란?- 변이형 오토인코더, VAE는 심층 신경망을 이용한 생성 모델의 하나로, 데이터의
jaylala.tistory.com
[생성 AI] 변이형 오토인코더(Variational Auto Encoder) (2/2)
[생성 AI] 변이형 오토인코더(Variational Auto Encoder) (2/2)
[해당 포스팅은 "만들면서 배우는 생성 AI 2탄"을 참조했습니다] 지난번에 알아본 개념을 바탕으로 이번에는 코드를 통해 실습을 해보겠습니다. 이번에 실습할 데이터는 패션 MNIST 데이터입니다
jaylala.tistory.com
[딥러닝 with Python] 변이형 오토인코더(Variational Auto Encoder) 추가본 - CelebA Faces 활용
[딥러닝 with Python] 변이형 오토인코더(Variational Auto Encoder) 추가본 - CelebA Faces 활용
[해당 포스팅은 "만들면서 배우는 생성 AI 2탄" 을 참조했습니다] 이번 지난번 2편의 변이형 오토 인코더에 대한 포스팅의 확장 버전입니다.[생성 AI] 변이형 오토인코더(Variational Auto Encoder) (1/2) [
jaylala.tistory.com
하지만, 노멀라이징 플로에서는 디코딩 함수는 인코딩 함수의 역함수를 활용하고 있기에 인코더와 디코더의 확률밀도 함수가 서로 같습니다.
노멀라이징 플로는 복잡한 확률 분포를 모델링하는데 사용되는 방법 중 하나로, 단순한 분포(정규분포)로부터 시작하여 일련의 가역 변환을 통해 목표 분포로 변형시키는 방식으로 작동하게 됩니다.
노멀라이징 플로는 다음과 같은 특징을 가지고 있는데요
1) 일반적으로 단순한 분포(다변량 정규 분포)에서 샘플을 생성하게 됩니다.
2) 변환
* 기본 분포에서 샘플된 데이터를 목표 분포로 변환하는 일련의 가역적(Invertible) 함수인 f1,f2, ....., fk를 적용합니다.
* 각 함수는 가역적(Invertible)이어야 하며, 야코비안을 계산할수 있어야 합니다.
3) 2)의 과정을 통해 변환된 샘플 분포는 목표 분포(Target Distribution)을 따르게 됩니다.
이때 변환 과정을 세부적으로 알아보면 다음과 같습니다.
노멀라이징 플로는 밀도 추정 문제에서도 유용하게 활용될 수 있습니다.
기분 분포의 확류 밀도함수인 pz(z)와 각 변환의 야코비안 행렬을 사용하여 목표 분포의 확률 밀도 px(x)를 계산할 수 있으며 이는 다음과 같은 식으로 표현됩니다.
이제 이렇게 알아본 Normalizing Flow 모델을 활용한 Real NVP 라는 모형을 파이썬 코딩을 통해서 구현해보겠ㅆ브니다.
RealNVP는 2017년 딘 등이 처음 소개했으며, 저자들은 복잡한 데이터 분포를 간단한 가우스 분포로 변환하는 신경망을 만드는 방법을 보여주었습니다. 또한 역변환이 가능하고 야코비안 행렬을 쉽게 계산할 수 있었는데요
먼저, output 디렉토리를 만들어줍니다.
import sys
# 코랩일 경우 노트북에서 output 디렉토리를 만듭니다.
if 'google.colab' in sys.modules :
! mkdir output
다음은 모델 구현을 위한 라이브러리르 들을임포트 해줍니다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
import tensorflow as tf
from tensorflow.keras import (
layers ,
models ,
regularizers ,
metrics ,
optimizers ,
callbacks ,
)
import tensorflow_probability as tfp
학습간 활용할 하이퍼 파라미터를 정의해줍니다.
COUPLING_DIM = 256
COUPLING_LAYERS = 6
INPUT_DIM = 2
REGULARIZATION = 0.01
BATCH_SIZE = 256
EPOCHS = 300
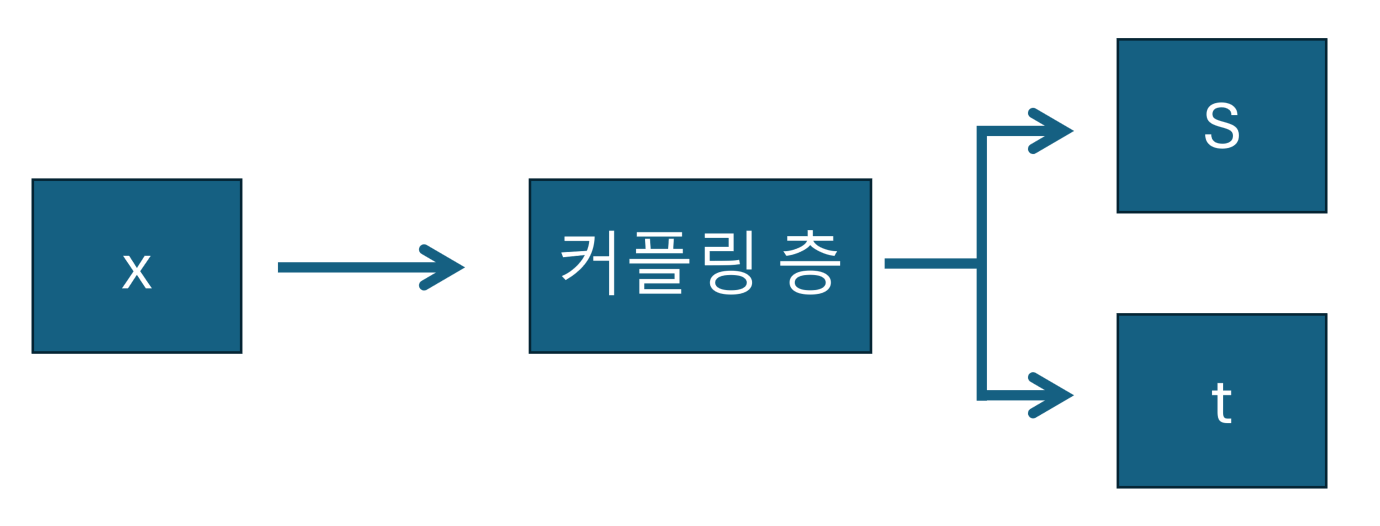
학습에 사용할 초승달 데이터셋을 로드해줍니다. 데이터는 사이킷 런 라이브러리의 make_moons 함수로 만들어줍니다.
# 데이터 로드
data = datasets.make_moons ( 30000 , noise= 0.05 )[ 0 ] .astype ( "float32" )
norm = layers.Normalization ()
norm.adapt ( data )
normalized_data = norm ( data )
plt.scatter (
normalized_data.numpy ()[:, 0 ], normalized_data.numpy ()[:, 1 ], c= "green"
)
plt.show ()
이제 Real NVP에서 사용되는 커플링 층을 정의해줍니다.
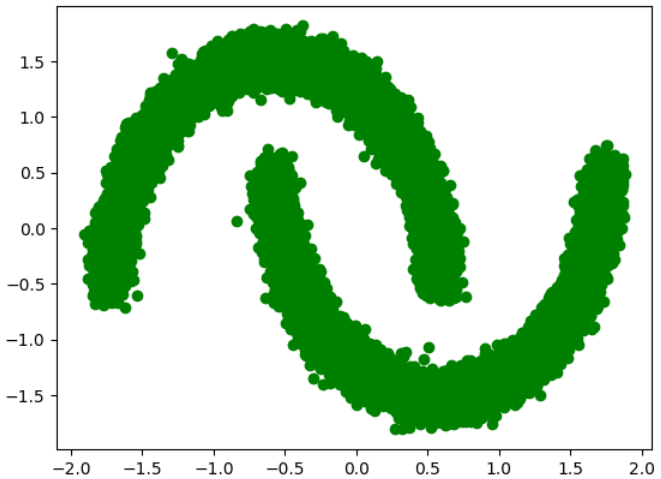
커플링 층은 입력의 각 원소에 대해서 스케일 계수와 이동 계수를 만들어줍니다. 이 층은 입력과 정확히 동일한 크기의 텐서 두개를 만들어줍니다. 이 중 하나는 스케일 계수(scale factor)이고 하나는 이동 계수(transition factor)입니다.
이를 코드로 구현하면 아래와 같습니다.
def Coupling ( input_dim , coupling_dim , reg ) :
input_layer = layers.Input ( shape=input_dim )
s_layer_1 = layers.Dense (
coupling_dim , activation= "relu" , kernel_regularizer=regularizers.l2 ( reg )
)( input_layer )
s_layer_2 = layers.Dense (
coupling_dim , activation= "relu" , kernel_regularizer=regularizers.l2 ( reg )
)( s_layer_1 )
s_layer_3 = layers.Dense (
coupling_dim , activation= "relu" , kernel_regularizer=regularizers.l2 ( reg )
)( s_layer_2 )
s_layer_4 = layers.Dense (
coupling_dim , activation= "relu" , kernel_regularizer=regularizers.l2 ( reg )
)( s_layer_3 )
s_layer_5 = layers.Dense (
input_dim , activation= "tanh" , kernel_regularizer=regularizers.l2 ( reg )
)( s_layer_4 )
t_layer_1 = layers.Dense (
coupling_dim , activation= "relu" , kernel_regularizer=regularizers.l2 ( reg )
)( input_layer )
t_layer_2 = layers.Dense (
coupling_dim , activation= "relu" , kernel_regularizer=regularizers.l2 ( reg )
)( t_layer_1 )
t_layer_3 = layers.Dense (
coupling_dim , activation= "relu" , kernel_regularizer=regularizers.l2 ( reg )
)( t_layer_2 )
t_layer_4 = layers.Dense (
coupling_dim , activation= "relu" , kernel_regularizer=regularizers.l2 ( reg )
)( t_layer_3 )
t_layer_5 = layers.Dense (
input_dim , activation= "linear" , kernel_regularizer=regularizers.l2 ( reg )
)( t_layer_4 )
return models.Model ( inputs=input_layer , outputs= [ s_layer_5 , t_layer_5 ])
* scale factor 는 s_layer 층으로, trainsition factor는 t_layer로 정의하고 하이퍼파라미터에서 정의된 coupling dimension을 가지는 층을 5개 쌓아줍니다. 이렇게 Dense 층을 쌓아줌으로써 학습을 위한 복잡성을 추가해줍니다.
* s_layer의 마지막 활성화 함수는 tanh 를 , t_layer의 마지막 활성화 함수는 linear 를 사용해줍니다.
* 이를 통해 최종 2개의 출력 (s 와 t) 이나오게 됩니다.
이제 커플링 층으로 데이터를 전달해보겠습니다.
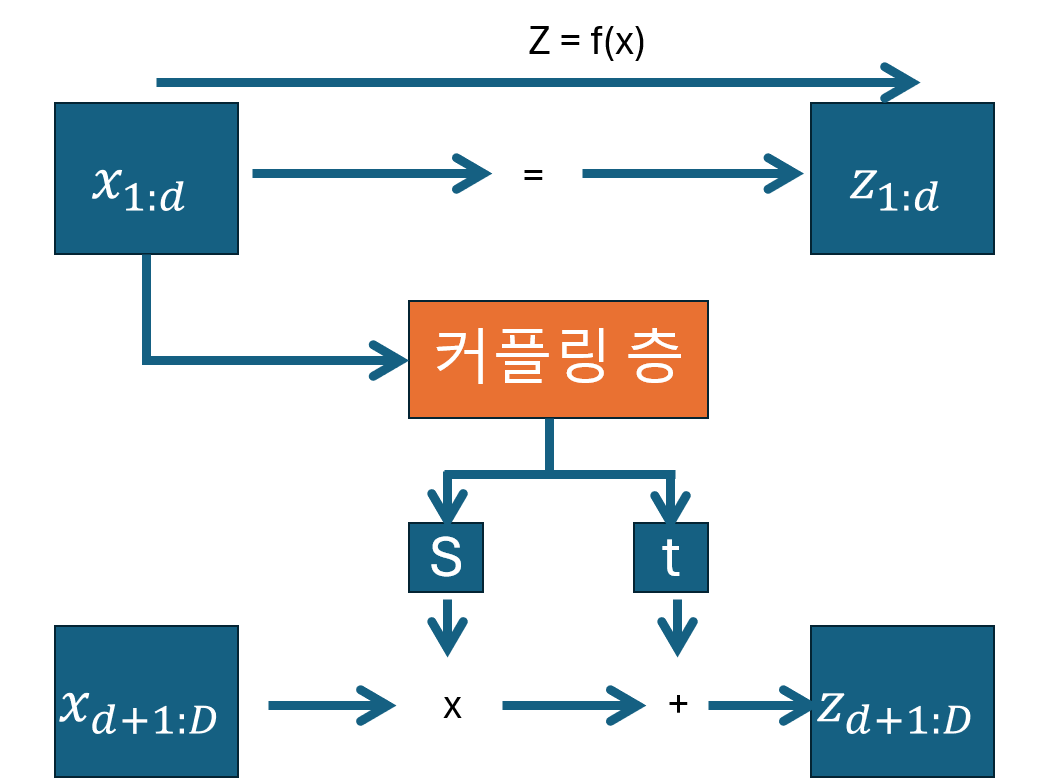
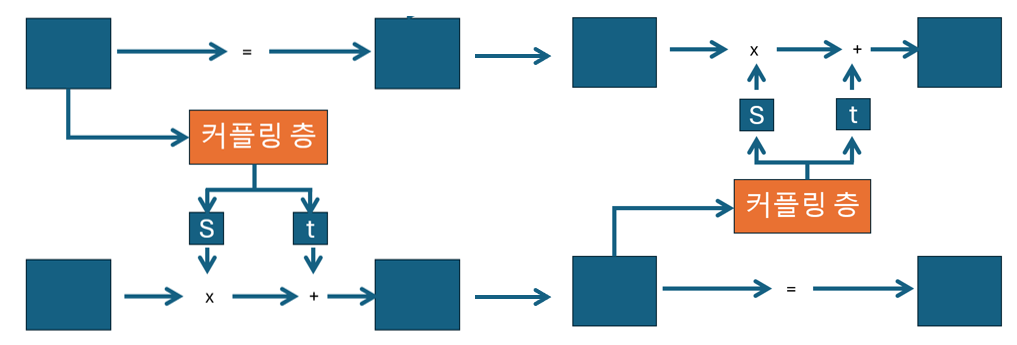
커플링 층을 통해 입력 x를 변환하는 과정은 아래 그림과 같습니다.
데이터의 처음 d 차원만 처음 커플링 층에 주입됩니다. 남은 D-d 차원은 완전히 마스킹 됩니다.(즉 0으로 설정)
D= 2 이고 d=1인 예제를 생각해보겠습니다.
이럴 경우, 커플링 층이 두개의 값 (x1, x2)이 아니라 (x1,0)을 보게 됩니다.
이 층의 출력은 스케일 곗와 이동 계수입니다. 이 값들이 다시 마스킹 되지만 이번에는 역 마스크를 사용해 두 번째 절반만 통과됩니다. 즉, 이 예제에서는 (0,s2)와 (0,t2)가 출력됩니다. 그런 다음 입력의 두 번째 절반인 x2에 원소별로 적용하고 입력의 첫 번째 절반인 x1은 업데이트하지 않고 그대로 통과 시킵니다. 요약하면 차원이 D 이고 d <D 인 벡터의 업데이트 식은 다음과 같습니다.
이때 마스킹 층을 만드는 이유는 하삼각행렬(Lower Triangle Matrix)를 만들기 위함입니다.
함삼각행렬은 아래와 같이 원소가 주대각선에 위치하고, 주대각선 위의 모든 원소는 0인 행렬을 의미합니다.
이를 활용하면 뚜렷한 장점이 하나 생기는데요 그것은 바로 행렬식의 주대각선의 원소들의 곱으로만 구해진다는 것입니다.
위에서 알아본 야코비안 행렬의 변환과정에서 행렬식을 쉽게 구할 수 있다는 장점이 생기게 되므로 위쪽부분을 없애는 마스킹을 한다고 보시면 되겠습니다.
이제 이를 역으로 하는 함수르 다음과 같이 정의하면
Real NVP 구현을 위한 최종과정이 완료됩니다.
이제 이 과정을 연속으로 이어주면 됩니다. 즉 커플링 층을 쌓으면 되는데요
아래와 같이 한 층에서 변경되지 안흔 부분이 다음 층에서 업데이트 되게 교차적인 구조로 업데이트 시켜가면 되겠습니다.
이를 구현한 RealNVP 모델입니다.
class RealNVP ( models . Model ) :
def __init__ (
self , input_dim , coupling_layers , coupling_dim , regularization
) :
super ( RealNVP , self ) . __init__ ()
self .coupling_layers = coupling_layers
self .distribution = tfp.distributions.MultivariateNormalDiag (
loc= [ 0.0 , 0.0 ], scale_diag= [ 1.0 , 1.0 ]
)
self .masks = np.array (
[[ 0 , 1 ], [ 1 , 0 ]] * ( coupling_layers // 2 ), dtype= "float32"
)
self .loss_tracker = metrics.Mean ( name= "loss" )
self .layers_list = [
Coupling ( input_dim , coupling_dim , regularization )
for i in range ( coupling_layers )
]
@property
def metrics ( self ) :
return [ self .loss_tracker ]
def call ( self , x , training = True ) :
log_det_inv = 0
direction = 1
if training :
direction = -1
for i in range ( self .coupling_layers )[:: direction ]:
x_masked = x * self .masks [ i ]
reversed_mask = 1 - self .masks [ i ]
s , t = self .layers_list [ i ]( x_masked )
s *= reversed_mask
t *= reversed_mask
gate = ( direction - 1 ) / 2
x = (
reversed_mask
* ( x * tf.exp ( direction * s ) + direction * t * tf.exp ( gate * s ))
+ x_masked
)
log_det_inv += gate * tf.reduce_sum ( s , axis= 1 )
return x , log_det_inv
def log_loss ( self , x ) :
y , logdet = self ( x )
log_likelihood = self .distribution.log_prob ( y ) + logdet
return -tf.reduce_mean ( log_likelihood )
def train_step ( self , data ) :
with tf.GradientTape () as tape :
loss = self .log_loss ( data )
g = tape.gradient ( loss , self .trainable_variables )
self .optimizer.apply_gradients ( zip ( g , self .trainable_variables ))
self .loss_tracker.update_state ( loss )
return { "loss" : self .loss_tracker.result ()}
def test_step ( self , data ) :
loss = self .log_loss ( data )
self .loss_tracker.update_state ( loss )
return { "loss" : self .loss_tracker.result ()}
model = RealNVP (
input_dim=INPUT_DIM ,
coupling_layers=COUPLING_LAYERS ,
coupling_dim=COUPLING_DIM ,
regularization=REGULARIZATION ,
)
이제 모델의 옵티마이저를 설정해주고
# 모델 컴파일 및 훈련
model. compile ( optimizer=optimizers.Adam ( learning_rate= 0.0001 ))
훈련 간 callbacks를 지정해주는데 이때 기록을 해주며, 그 기록은 데이터 분포의 시각적인 변환이 되겠습니다.
tensorboard_callback = callbacks.TensorBoard ( log_dir= "./logs" )
class ImageGenerator ( callbacks . Callback ) :
def __init__ ( self , num_samples ) :
self .num_samples = num_samples
def generate ( self ) :
# 데이터에서 잠재 공간까지.
z , _ = model ( normalized_data )
# 잠재 공간에서 데이터까지.
samples = model.distribution.sample ( self .num_samples )
x , _ = model.predict ( samples , verbose= 0 )
return x , z , samples
def display ( self , x , z , samples , save_to = None ) :
f , axes = plt.subplots ( 2 , 2 )
f.set_size_inches ( 8 , 5 )
axes [ 0 , 0 ] .scatter (
normalized_data [:, 0 ], normalized_data [:, 1 ], color= "r" , s= 1
)
axes [ 0 , 0 ] . set ( title= "Data space X" , xlabel= "x_1" , ylabel= "x_2" )
axes [ 0 , 0 ] .set_xlim ([ -2 , 2 ])
axes [ 0 , 0 ] .set_ylim ([ -2 , 2 ])
axes [ 0 , 1 ] .scatter ( z [:, 0 ], z [:, 1 ], color= "r" , s= 1 )
axes [ 0 , 1 ] . set ( title= "f(X)" , xlabel= "z_1" , ylabel= "z_2" )
axes [ 0 , 1 ] .set_xlim ([ -2 , 2 ])
axes [ 0 , 1 ] .set_ylim ([ -2 , 2 ])
axes [ 1 , 0 ] .scatter ( samples [:, 0 ], samples [:, 1 ], color= "g" , s= 1 )
axes [ 1 , 0 ] . set ( title= "Latent space Z" , xlabel= "z_1" , ylabel= "z_2" )
axes [ 1 , 0 ] .set_xlim ([ -2 , 2 ])
axes [ 1 , 0 ] .set_ylim ([ -2 , 2 ])
axes [ 1 , 1 ] .scatter ( x [:, 0 ], x [:, 1 ], color= "g" , s= 1 )
axes [ 1 , 1 ] . set ( title= "g(Z)" , xlabel= "x_1" , ylabel= "x_2" )
axes [ 1 , 1 ] .set_xlim ([ -2 , 2 ])
axes [ 1 , 1 ] .set_ylim ([ -2 , 2 ])
plt.subplots_adjust ( wspace= 0.3 , hspace= 0.6 )
if save_to :
plt.savefig ( save_to )
print ( f "\nSaved to { save_to } " )
plt.show ()
def on_epoch_end ( self , epoch , logs = None ) :
if epoch % 10 == 0 :
x , z , samples = self .generate ()
self .display (
x ,
z ,
samples ,
save_to= "./output/generated_img_%03d.png" % ( epoch ),
)
img_generator_callback = ImageGenerator ( num_samples= 3000 )
이제 모델을 실행하면
model.fit (
normalized_data ,
batch_size=BATCH_SIZE ,
epochs=EPOCHS ,
callbacks= [ tensorboard_callback , img_generator_callback ],
)
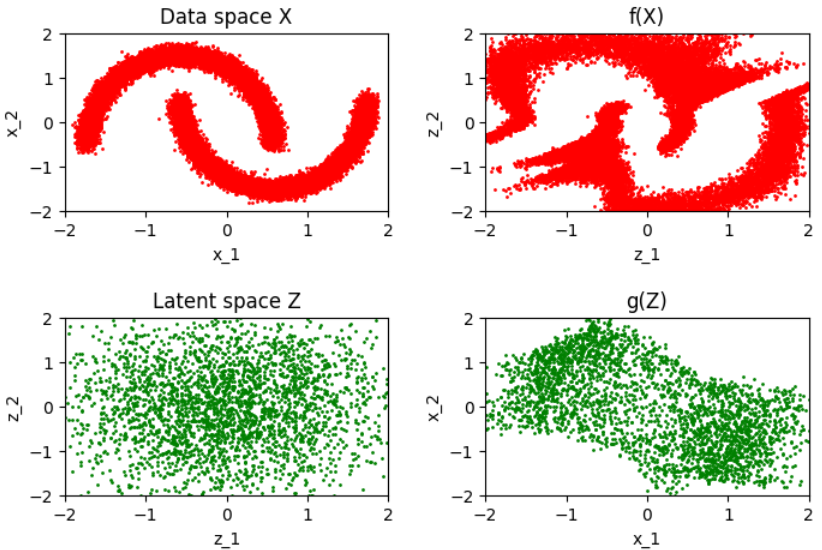
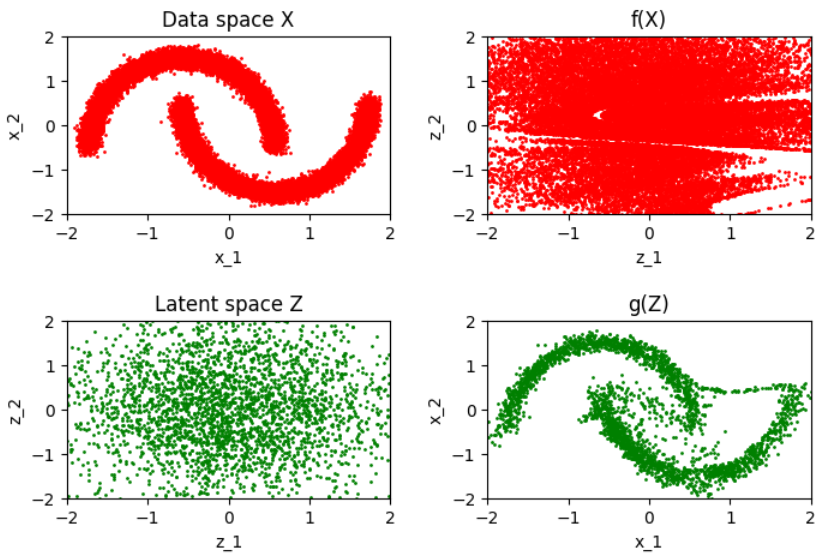
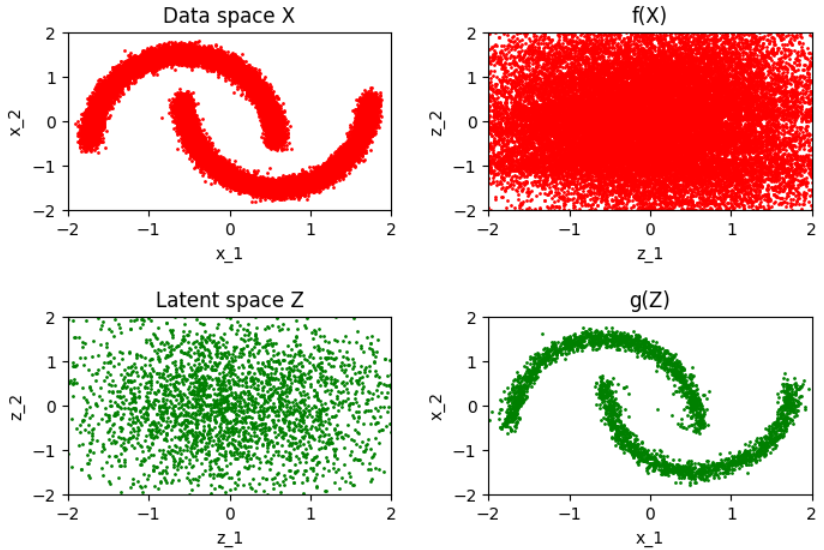
아래와 같은 결과가 나옵니다.
훈련이 된후 정방향 과정의 훈련 세테으 있는 포인트를 가우스 분포와 닮은 분포로 변환시켜줍니다.
[ 정방향 과정(빨간색)과 역방향 과정(초록색) 에대한 훈련 전의 Real NVP 모델 입력(왼쪽)과 출력(오른쪽) ]



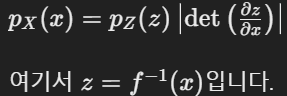
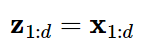
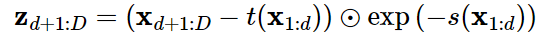
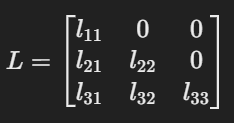
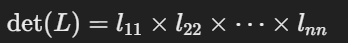
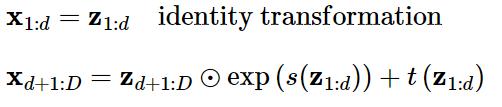




댓글