
[본 포스팅은 "ShapeNet : A Shapelet-Neural Network Approach for Multivariate Time Series Classification"(AAAI 2021 / Li et al.) 을 리뷰하였습니다]
이번에 알아볼 논문은 시계열 데이터 분류에서 활용되는 Shapelet을 효과적으로 추출하는 Neural Net을 제시하는 " ShapeNet : A Shapelet-Neural Network Approach for Multivariate Time Series Classification" 입니다.
Shapelet은 시계열 분류에서 특정 클래스와 다른 클래스를 구분하는 특정 클래스의 부분 시계열이라고 보시면 되겠습니다.
이에 대한 자세한 내용은 이전 포스팅을 참고바랍니다.
특히 Shapelet은 다중 채널에서 나오는 정보를 데이터화한 Multivariate Time Series 데이터를 분류하는 Task 입니다.
이상 간략한 소개였고, 다음은 Shapelet에서 제시하는 방법론에 대해서 자세히 알아보겠습니다.
1. ShapeNet
- ShapeNet은 다변량 시계열 분류(Multivariate Time Series Time Series Classification / MTSC)에서 Shapelet 기반 접근 방식을 딥러닝 네트워크와 결합한 방법입니다.
- 이때, Shapelet이란 시계열 데이터의 짧은 부분 구간(subsequence)을 의미하는 것으로, 해당 클래스(C target)와 다른 클래스(C others)를 구분짓는데 역할이 큰 해당 클래스(C target)의 부분 구간이 되겠습니다.
- 하지만, Shapelet에 대한 길이는 모델을 구상하는 사용자가 직접 찾아야하다 보니 엄청난 Computing cost가 필요하다는 단점이 있습니다. 특히, 이 문제는 다변량(다채널)로 들어가면 채널의 수 만큼 그 Cost가 배로 들것입니다.
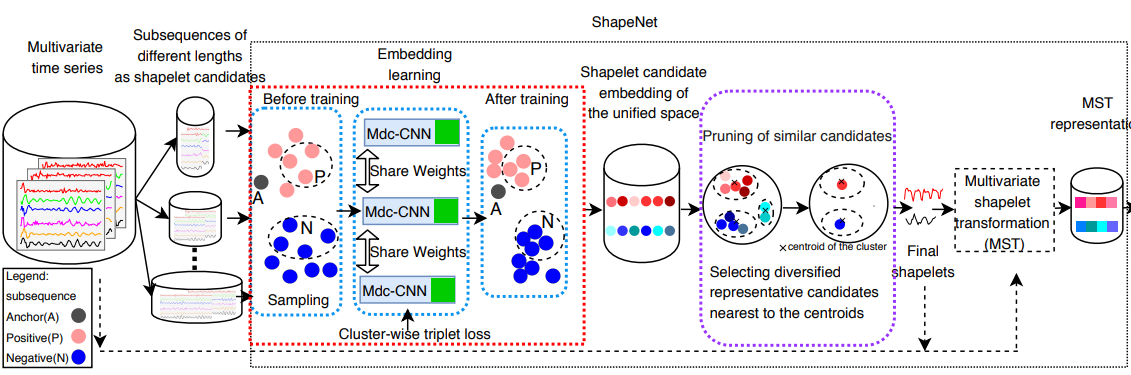
- 이를 해결하고자, ShapeNet은 효과적으로 Shapelet을 추출하는 기법을 제안하였습니다. ShapeNet의 전반적인 Architecture는 아래와 같습니다.

* 크게 단계를 나누어보면
1) Shapelet Candidates Generation (Shapelet 후보 생성)
2) Shapelet 임베딩 (Mdc -CNN 활용)
이때, Mdc-CNN이란, Multi length input Dilated Causal CNN을 뜻합니다.
3) Cluster - Wise Triplet Loss 기반 학습
4) Shapelet 후보군의 선택 및 다양화
5) 다변량 Shapelet으로 변환
6) 일반적인 분류기로 분류 (ex. SVM)
으로 나누어볼 수 있습니다.
* 그림에서도 보실 수 있듯이 ShapeNet이라고 하는 부분은 2) Shapelet 임베딩 ~ 5) 다변량 Shapelet으로 변환 이라는 부분으로 보시면 되겠습니다.
- 방법론을 자세히 알아보면 아래와 같습니다.
1) Shapelet 후보 생성(Shapelet Candidates Generation)

* 해당 단계에서는 여러 채널로부터 다양한 길이의 Shapelet을 생성하여, 학습에 사용할 Shapelet 후보군을 만드는 과정입니다. 이때, Sliding window 기법을 활용합니다.
* 그림에서 보시는 것처럼 다양한 길이의 Shapelet 후보군을 생성하게 됩니다. 길이가 짧을수록 분할된 구간의 숫자가 더 많아지며, 길이가 길수록 분할된 구간의 숫자가 적어짐을 알 수있습니다.
* 이때, 짧은 길이는 국소적인 패턴을 / 긴 길이는 전반적인 패턴을 찾는데 적합합니다.
2) Shapelet 임베딩(Mdc-CNN 활용)

* 생성된 Shapelet 후보군은 다양한 길이와 변수를 가지기 때문에 이를 동일한 공간에서 비교하는 것이 어렵습니다. 이를 해결하기 위해, Mdc-CNN (Multi length input Dilated Causal CNN) 이라는 모델을 활용했씁니다.
* Mdc-CNN은 확장된 커널(Dilated Kernel)을 통해 시계열 데이터를 처리한 뒤, 다양한 길이의 Shapelet 후보들을 하나의 통일된 공간으로 임베딩 하기 위해 사용됩니다. 이는 아래 그림으로 이해해볼 수 있습니다.

* Causal Convolution은 현재 시점에서 과거 데이터만을 사용하여 연산을 수행하는 방식을 의미합니다.
* Dialation conv를 활용 시 넓은 수용 영역(Receptive Field)을 다룰 수 있다는 점에서 시계열 데이터의 long-term dependency를 학습하는데 유리할 수 있습니다. 하지만, 일반적인 Dilation Conv를 활용 시, 시계열 데이터에서의 일반적인 가정(미래시점의 정보는 과거시점에 영향을 미치지 않는다)를 위배하게 됩니다. 이는 아래 그림을 통해서 쉽게 알아볼 수 있습니다.
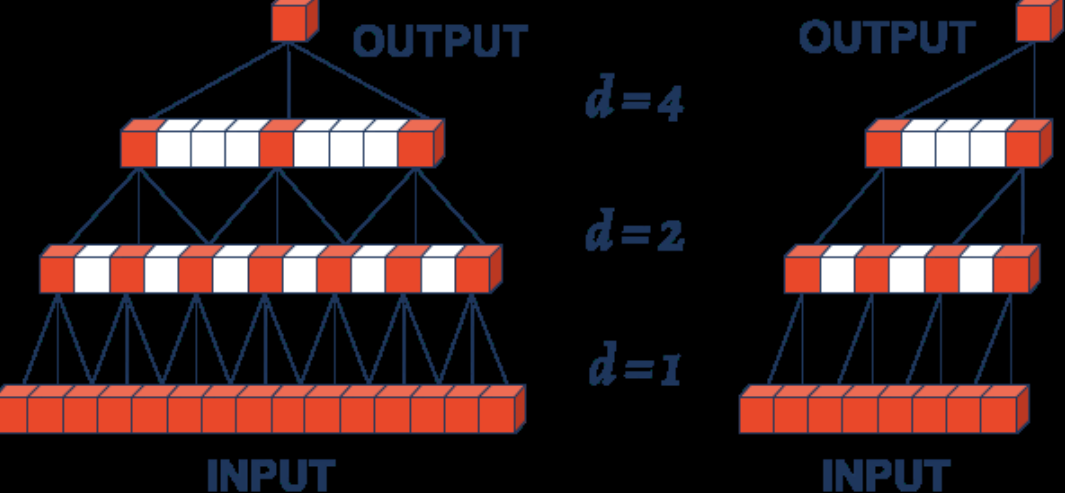
* 왼쪽은 일반적인 Dilated Convolution이고, 오른쪽은 Causal Dialated Convolution입니다. 왼쪽 그림(Dilated Conv)의 경우 과거와 미래 시점의 데이터를 모두 사용해 합성곱을 수행하지만, 오른쪽 그림(Dilated Causal Conv)는 과거 시점의 정보만을 가지고 학습을 진행하기에 일반적인 시계열 데이터의 가정을 위반하지 않게 되는 것입니다.
* 이와 같은 개념을 활용해 embedding을 하게되는 architecture는 아래와 같습니다.
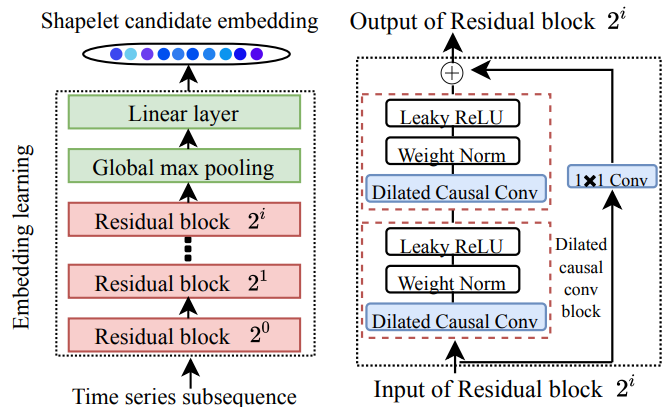
Residual Block들은 각기 다른 dilation factor를 가지는 Dilated Causal Convolution으로 구성되며, 각 블록안에서 Dilated Causal Conv => Weight Normalization => Leaky ReLU의 순으로 연산이 두번 반복됩니다. 이를 활용하게 되면 과거 정보만을 사용해 현재 시점의 출려을 계산하는 인과적 특성을 유지하면서, 다양한 시간 범위의 패턴을 학습할 수 있도록 해줍니다.
이후 Global Max Pooling을 통해 각 시점에서 가장 중요한 정보를 추출하여 시계열 데이터의 전역적인 요약 정보를 얻게 되고, 이렇게 요약된 정보는 Linear Layer를 거쳐 다양한 채널정보를 통합된 임베딩 벡터를 원하는 크기만큼 생성할 수 있게 됩니다.
3) Cluster-wise Triplet Loss
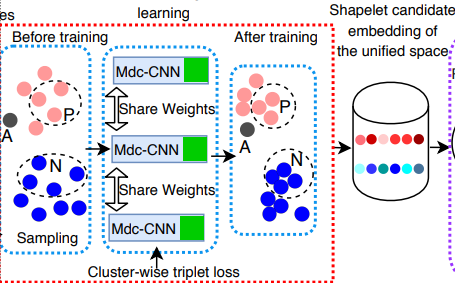
* 2)에서 정의된 모델을 활용해서 임베딩이 도출되지만 이 임베딩에 대한 학습이 효과적으로 이루어지기 위해 Cluster-Wise Triplet Loss를 활용합니다.
* 이때 Triplet Loss란, 임베딩 학습에서 자주 사용되는 손실 함수로, Anchor / Positive / Negative 라는 3개의 샘플 간의 관계를 고려하는 손실을 의미합니다.
Anchor(기준 샘플)은 임베딩 공간에서 비교의 기준이 되는 샘플을 말하며, Positive(양성 샘플)은 Anchor와 같은 클래스에 속하는 샘플을, Negative(음성 샘플)은 Anchor와 다른 클래스에 속하는 샘플을 말합니다.
이를 활용해 Anchor와 Positive 샘플간의 거리는 가깝고, Anchor와 Negative 샘플간의 거리는 멀게 만들어야 하는데 이를 수식으로 정의한 손실함수는 아래와 같습니다.

*Shape Net에서 활용되는 Cluster-Wise Triplet Loss는 여러개의 Positive 및 Negative 샘플간의 관계를 동시에 학습하는 손실 함수를 말합니다.
* 이를 통해, 같은 Class에서 나온 Shapelet이더라도 시계열 데이터의 서로 다른 구간을 나타내기 때문에 임베딩 공간에서 서로 다른 위치에 매핑 될 수 있습니다.
* 즉, 똑같은 클래스의 Shapelet이라도 해당 클래스의 특징을 더 잘 반영하는 Shapelet일수록 Anchor와 가까워질 것이고, 덜 중요한 패턴을 담고 있는 Shapelet은 Anchor와 더 멀어지게 될 것입니다.
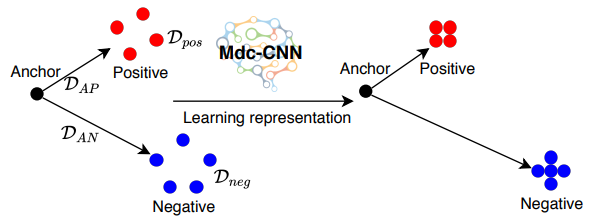
* 이를 수식을 통해서 알아보면 아래와 같이 정리할 수 있습니다.



4) Shapelet 후보군의 선택 및 다양화
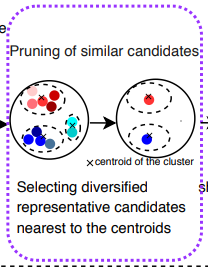
* 2)~3)을 통해 Shapelet에 대한 후보군을 임베딩한 후, 클러스터링 기법을 활용해 유사한 shapelet을 그룹화하고, 그 중에서 대표적이고 다양한 shapelet을 선택합니다. 이는 K-Means Clustering을 활용해 이루어지며, 각 클러스터의 중심에 가까운 Shapelet을 최종 선택하여 최종 Shapelet 후보군을 선택합니다.
5) 다변량 Shapelet 변환(Multivariate Shapelet Transformation)
* 최종적으로 선택된 Shapelet들을 사용해 다변량 시계열 데이터를 다변량 Shapelet으로 변환합니다. 각 시계열 데이터는 선택된 Shapelet과의 거리를 계산해 새로운 특징 공간으로 변환되고, 이 과정을 통해 다변량 시계열 데이터는 각 Shapelet과의 거리 요소를 가지는 벡터로 변환됩니다.
6) Standard한 분류기를 활용해 최종 분류
* 해당 논문에서는 SVM을 활용해 최종 분류를 진행했습니다.
2. 결과
- UEA Archive에 있는 30개의 데이터에 대해서 각각 Accuracy를 구해보았고,아래와 같은 방식으로 비교하였습니다.
* Total best acc : 전체 데이터 셋 중에서 해당 모델이 Best Accuracy인 데이터 셋은 몇개인가?
* Ours 1-to-1 Wins : ShapeNet과 기존 모델을 1 대 1 비교를 했을때 해당 모델이 이긴 데이터셋은 몇개인가?
* Ours 1-to-1 Drawas : ShapeNet과 기존 모델을 1 대 1 비교를 했을때 비긴 경우는 몇개인가?
* Ours 1-to-1 Losses : ShapeNet과 기존 모델을 1 대 1 비교를 했을때 진 경우는 몇개인가?
* Rank Mean : 각 데이터 셋 별 Accuracy 성과를 전체 모델을 기준으로 Ranking을 매겼을때, 평균 Ranking은?
* Wilcoxon Test p-value : ShapeNet의 결과들과 해당 모델의 결과를 가지고, 두 모델간의 결과 차이가 유의미한가?
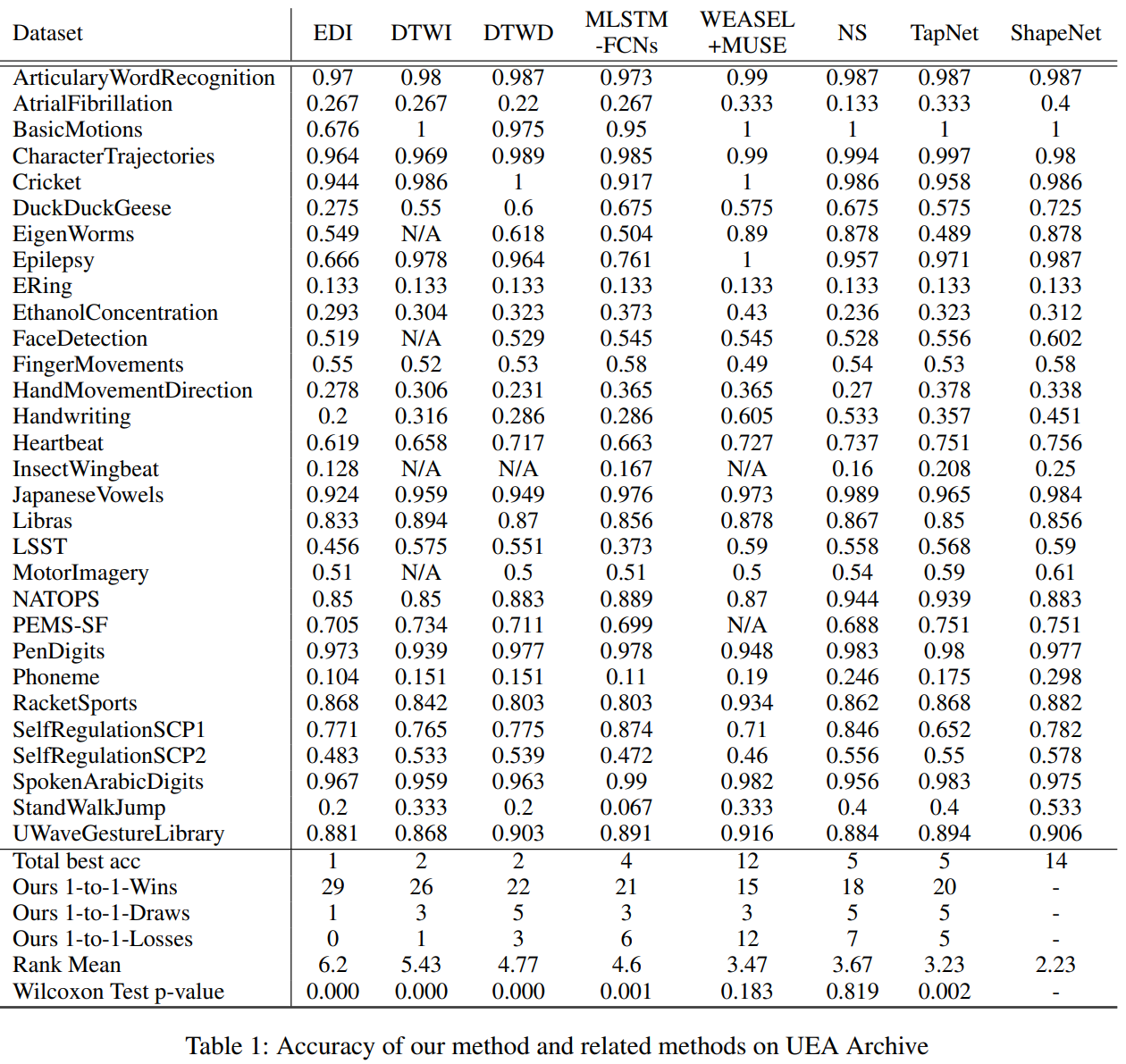
결과적으로 best Accuracy가 가장 많고 wins/draws/losses를 비교했을때도 좋으며, Rank Mean도 가장 높고, WEASEL+MUSE와 NS를 제외하고는 모두 두 모델의 정확도 결과의 차이가 유의미함을 나타내고 있습니다.
'딥러닝 with Python' 카테고리의 다른 글
| [딥러닝 with Python] VAE (Variational Auto Encoder) 개념 정리 (1) | 2024.10.28 |
|---|---|
| [딥러닝 with Python] GELU란?(Gaussian Error Linear Unit) (0) | 2024.10.27 |
| [개념 정리] Shapelet이란? (시계열 분류) (0) | 2024.10.25 |
| [딥러닝 with Python] Mexican Hat Wavelet Transform을 활용한 시계열 데이터 처리 (0) | 2024.10.24 |
| [딥러닝 with Python] TSFEL(Time Series Feature Extraction Library) / 시계열 특징 추출 라이브러리 (2) | 2024.10.18 |




댓글