[딥러닝 with Python] GELU란?(Gaussian Error Linear Unit)

이번에 알아볼 것은 활성화 함수로 활용되는 GELU에 대해서 알아보겠습니다.

 

1. GELU란?

- GELU는 Gaussian Error Linear Unit의 줄임말로, 딥러닝에서 활용되는 비선형 활성화 함수 중의 하나입니다.

 

- 기존 활성화함수인 ReLU나 Sigmoid에 비해 더 부드럽게 동작한다고 얘기할 수있는데요. 이는, 큰 값일수록 활성화 될 확률이 높고, 작은 값일수록 활성화될 확률이 낮아지는 형태를 취하기 때문입니다.

 

- GELU를 활용해서 좋은 성능을 보인 대표적 모델은 BERT가 되겠습니다.

 

 

- GELU의 공식은 아래와 같습니다.

 

 

- 이를 조금 더 간단히 근사해보면 아래와 같습니다.

 

- 그렇다면, 이 함수가 어떤 형태를 띄는지 2차원에서 시각화해보도록 하겠습니다.

* 파이썬을 활용해서 함수를 정의하고 시각화 해보겠습니다.

import numpy as np

import matplotlib.pyplot as plt

# GELU 함수 정의

def gelu(x):

    return 0.5 * x * (1 + np.tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * x**3)))

# x 값 범위 설정

x = np.linspace(-5, 5, 100)

# y 값으로 GELU 계산

y = gelu(x)

# 시각화

plt.figure(figsize=(8, 6))

plt.plot(x, y, label="GELU", color='b')

plt.title("GELU Activation Function")

plt.xlabel("Input")

plt.ylabel("Output")

plt.grid(True)

plt.legend()

plt.show()

 

 

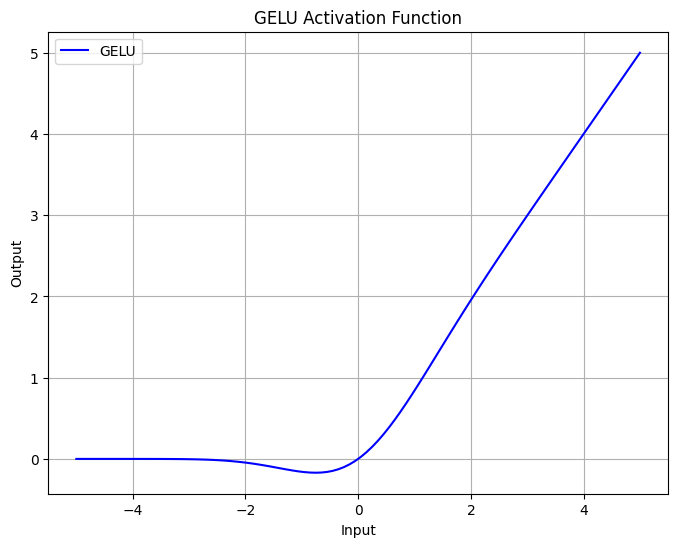
- 위 그림을 보시면, 양의 값을 가지는 부분은 잘 활성화가 되고, 음의 값을 가지는 부분은 0 근처에서 일부 음의 값을 가지다 0보다 더 멀어지게 되면 0에 가까워지는 것을 보실 수 있습니다.

 

- 이번에는 ReLU 및 sigmoid와 함께 비교해서 그려보겠습니다.

import numpy as np

import matplotlib.pyplot as plt

# 다양한 활성화 함수 정의

def gelu(x):

    return 0.5 * x * (1 + np.tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * x**3)))

def relu(x):

    return np.maximum(0, x)

def sigmoid(x):

    return 1 / (1 + np.exp(-x))

# x 값 범위 설정

x = np.linspace(-5, 5, 100)

# y 값으로 활성화 함수 계산

y_gelu = gelu(x)

y_relu = relu(x)

y_sigmoid = sigmoid(x)

# 시각화 (GELU, ReLU, Sigmoid만 비교)

plt.figure(figsize=(10, 8))

# GELU, ReLU, Sigmoid 그래프 그리기

plt.plot(x, y_gelu, label="GELU", color='b', linewidth=3)

plt.plot(x, y_relu, label="ReLU", color='g', linestyle='--')

plt.plot(x, y_sigmoid, label="Sigmoid", color='r', linestyle='--')

# 그래프 설정

plt.title("Comparison of GELU, ReLU, and Sigmoid")

plt.xlabel("Input")

plt.ylabel("Output")

plt.grid(True)

plt.legend()

plt.show()

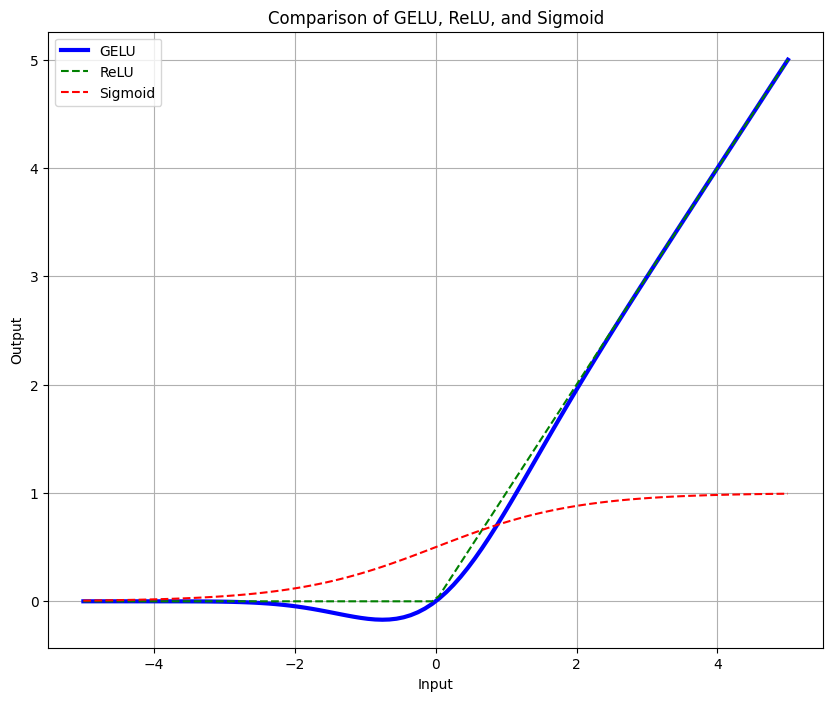
- 비교한 그림을 보니 이제 좀 차이를 확인할 수 있습니다. Sigmoid에 비해서는 양의값에서 활성화되는 비율이 확연히 다름을 알 수 있고, ReLU에 비해서는 음의 값에 대해서 일부 반영해주는 부드러운 곡선을 보여주고 있습니다.

 

2. GELU를 사용하는 이유

- GELU를 사용하는 이유는 여러가지가 있을 수 있겠으나 요약해보면 아래와 같습니다.

 

1) 확률적 활성화 

 * GELU는 입력값의 크기에 따라 확률적으로 활성화가 결정되며, 큰 값일수록 활성화될 확률이 높고 작은 값일수록 낮습니다. 이는 ReLU의 단순한 활성화방식보다 부드럽게 동작하기에 NLP 모델에서 자주 활용됩니다.

 * 이때, 여기서 말하는 확률적 활성화란 단순히 값이 0 또는 1로 나누어지는 것이 아니라 특정 분포를 기반으로 부드럽게 결정된다는 것을 말합니다. GELU에서는 표준정규분포의 누적분포함수(CDF)를 통해 활성화된 값을 출력하기에 이를 통해 입력값이 클수록 활성화될 확률이 높아지고, 작을수록 비활성화될 확률이 높아지게 됩니다.

 

2) 부드러운 비선형성

 * ReLU는 0에서 갑작스런 활성화 값의 변화가 생기나, ReLU의 경우 경계에서 갑작스런 변화없이 연속적이고 부드럽게 동작하게 됩니다.

 

3) Swish 활성화 함수(SiLU)와 비교 시, 계산 비용이 적음

 * GeLU는 Swish 활성화 함수와 비교했을 때 계산 비용이 더 적다는 장점이 있는데요 

[개념정리] SiLU(Sigmoid Linear Unit) 활성화 함수

[개념정리] SiLU(Sigmoid Linear Unit) 활성화 함수

 

 * Swish 활성화 함수는 다음과 같은데요 

 

* 여기서 컴퓨팅 적인 측면에서 봤을때, Sigmoid 함수는 지수함수를 계산해야한다는 부분 때문에 GeLU보다는 상대적으로 계산 비용이 높은 편입니다.