
이번에는 회귀 함수를 기반으로 하지 않고 결정 트리와 같이 트리를 기반으로 하는 회귀방식인, 회귀 트리(Regression Tree)에 대해서 알아보겠습니다.
분류에 사용되는 결정 트리에 관한 내용은 아래 포스팅을 참조하시면 도움이 되실 겁니다!
[머신러닝 with Python] 결정 트리(Decision Tree) (1/2) / 결정트리 시각화(Graphviz 활용) / 붓꽃(iris) 데이터
[머신러닝 with Python] 결정 트리(Decision Tree) (1/2) / 결정트리 시각화(Graphviz 활용) / 붓꽃(iris) 데이터
이번에 알아볼 것은 분류(Classification) 모델의 대표격인 결정트리 / 결정나무 (Decision Tree) 입니다. 1. 결정트리 / 결정나무(Decision Tree)란? - 결정트리(Decision Tree)는 머신러닝 알고리즘 중 직관적으로
jaylala.tistory.com
1. 회귀 트리(Regression Tree)란?
- 회귀 트리(Regression tree)는 의사 결정 트리(Decision Tree)의 일종이며, 입력 특징에 대한 조건들을 사용하여 데이터를 분할하고 각 분할된 영역에서 평균값을 예측하여 회귀 문제를 해결하는 방법입니다.
- 아래 그림을 통해서 선형회귀와 회귀트리의 차이를 확인하실 수 있습니다.
* 똑같은 데이터를 가지고 선형 회귀(첫 번째)와 회귀트리(두 번째)를 한 결과를 2차원으로 시각화 한 모습입니다.
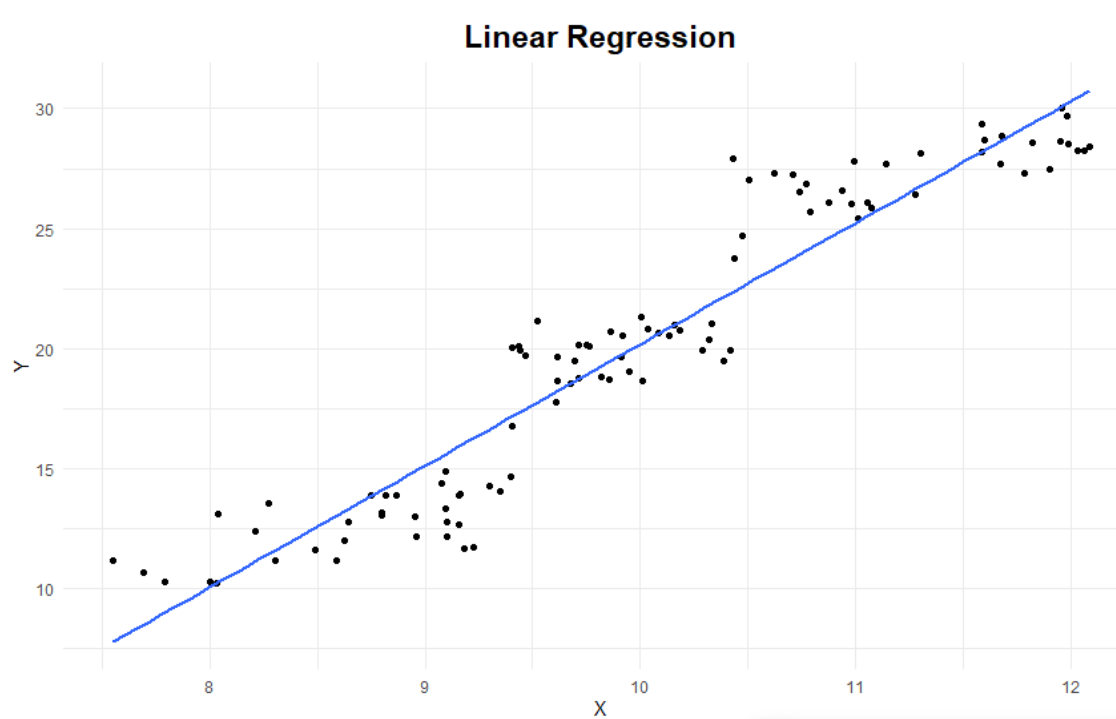
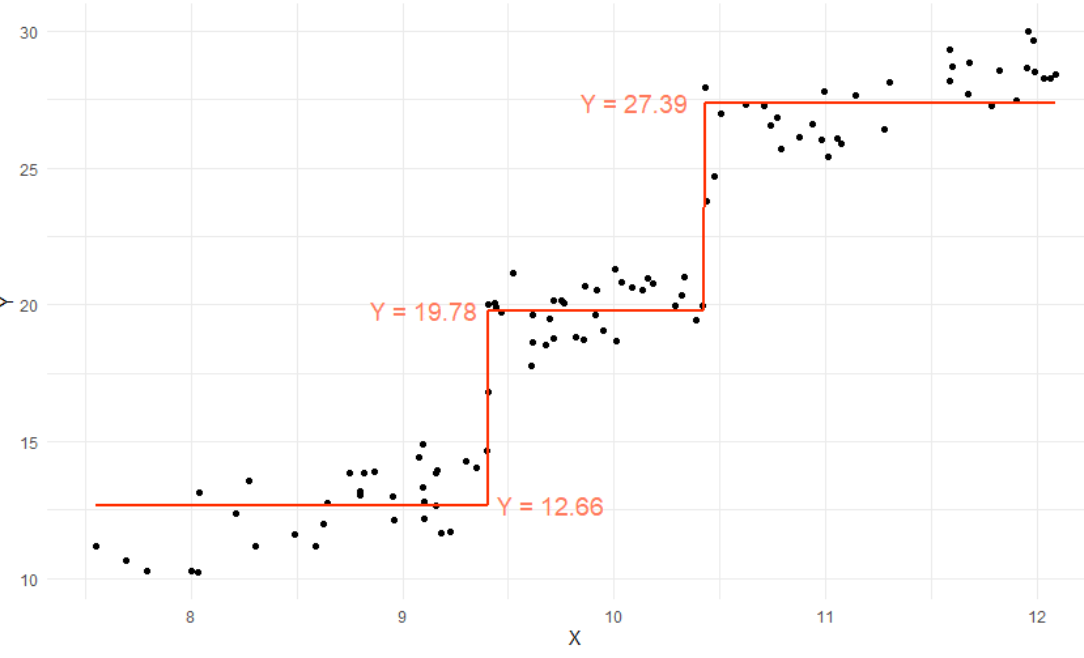
* 위 그림에서 알 수 있듯이 회귀트리는 각 데이터들이 유사한 y값으로 모여있는 부분으로 구역을 나눈 뒤 해당 구역에서 y값들의 평균값을 x축에 평행한 선을 그어 나타냈고, 이 선들을 이어서 계단형태의 분류트리를 만들어 냈습니다.
* 이와 같은 원리로 회귀 트리가 작동하기에 선형 회귀와 회귀 트리는 각 데이터의 특성에 따라 회귀 성능이 어떤 것이 더 좋을 수도 혹은 나쁠 수도 있는 것입니다.
- 다음은 회귀 트리의 주요 특징 및 작동 원리에 대해서 정리해 보았습니다.
a) 트리 구조: 회귀 트리는 의사 결정 트리와 마찬가지로 트리 구조를 가집니다. 이진 트리 형태로 구성되며, 각 노드는 특정 특징(feature)과 해당 특징의 임계값(threshold)을 기반으로 데이터를 분할합니다.
b) 분할 조건: 각 노드에서 데이터를 분할하기 위한 조건은 특징과 임계값으로 정의됩니다. 이 조건을 통해 데이터는 두 개의 하위 노드로 나뉩니다.
c) Leaf 노드: 더 이상 분할할 수 없는 노드를 잎 노드(leaf node)라고 합니다. 잎 노드에서는 해당 영역의 평균 값 또는 예측 값을 반환합니다.
d) 분할 알고리즘: 회귀 트리는 각 노드에서 분할을 결정하는 알고리즘을 사용합니다. 분할 알고리즘은 각 노드에서 가장 좋은 특징과 임계값을 선택하여 데이터를 분할합니다. 분할 기준은 주로 평균 제곱 오차(Mean Squared Error, MSE)나 평균 절대 오차(Mean Absolute Error, MAE)를 최소화하는 방향으로 선택됩니다.
e) 과적합 제어: 회귀 트리도 의사 결정 트리와 마찬가지로 과적합(Overfitting) 문제에 취약할 수 있습니다. 따라서 트리의 깊이나 분할 기준을 제한하는 하이퍼파라미터를 조정하여 과적합을 제어할 수 있습니다.
f) 예측: 새로운 입력 데이터가 주어지면 회귀 트리는 해당 데이터가 속한 잎 노드에서의 평균 값 또는 예측 값을 반환하여 회귀 문제를 해결합니다.
2. 파이썬 코딩을 통해 알아보는 회귀 트리(Regression Tree)
- 이번에는 임의의 예제를 생성해보고 해당 데이터를 활용해 회귀트리를 만들고 이를 시각화해보겠습니다.
* 먼저, 임의이 데이터를 만들고 회귀 트리 모델을 훈련 시킨 뒤 해당 데이터가 어떻게 데이터들을 예측하는 회귀선을 만들었는지 시각화 해보는 코드입니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
# 랜덤한 2차원 데이터 생성
np.random.seed(0)
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel() + np.random.normal(0, 0.1, X.shape[0])
# 의사 결정 트리 모델 생성 및 훈련
regr_1 = DecisionTreeRegressor(max_depth=2)
regr_2 = DecisionTreeRegressor(max_depth=5)
regr_1.fit(X, y)
regr_2.fit(X, y)
# 데이터를 y축을 기준으로 정렬
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_1 = regr_1.predict(X_test)
y_2 = regr_2.predict(X_test)
# 데이터 시각화
plt.figure()
# 구분선 표시
plt.plot(X_test, y_1, color="cornflowerblue", linestyle="--", label="max_depth=2")
plt.plot(X_test, y_2, color="yellowgreen", linestyle="--", label="max_depth=5")
plt.scatter(X, y, s=20, edgecolor="black", c="darkorange", label="data")
plt.xlabel("data")
plt.ylabel("target")
plt.title("Decision Tree Regression")
plt.legend()
plt.show()
|
cs |
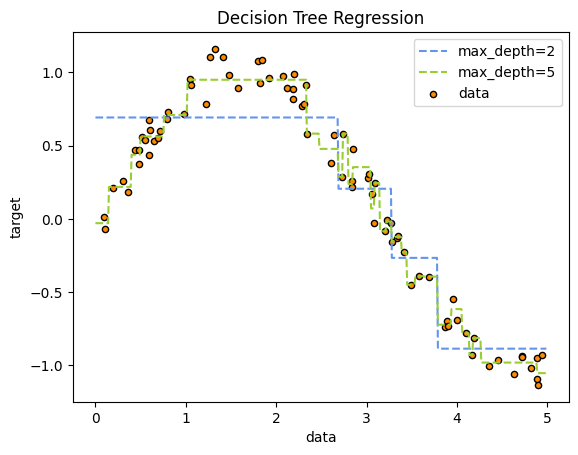
* max_depth가 2일때 보다 5일때 더 데이터들의 값을 유사하게 예측하는 모델이 나옴을 확인할 수 있습니다. 하지만, depth가 깊어질수록 과적합(Over-fitting) 문제가 발생하니 train / test split을 통해 적절한 깊이를 확인해야합니다.
* 다음은 위 결과를 만들었을때 사용된 논리, 즉 노드와 리프들의 형태에 대해서 graphviz를 통해 시각화 해보았습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
from sklearn.tree import export_graphviz
import graphviz
# max_depth=2인 의사 결정 트리 그래프 출력
dot_data_1 = export_graphviz(regr_1, out_file=None,
feature_names=["X"],
filled=True, rounded=True,
special_characters=True)
# max_depth=5인 의사 결정 트리 그래프 출력
dot_data_2 = export_graphviz(regr_2, out_file=None,
feature_names=["X"],
filled=True, rounded=True,
special_characters=True)
|
cs |
|
1
2
3
4
5
6
7
8
|
# max_depth=2인 의사 결정 트리 그래프 시각화 및 저장
graph_1 = graphviz.Source(dot_data_1)
graph_1.render("decision_tree_max_depth_2")
# max_depth=5인 의사 결정 트리 그래프 시각화 및 저장
graph_2 = graphviz.Source(dot_data_2)
graph_2.render("decision_tree_max_depth_5")
|
cs |






댓글