
이번에 알아볼 것은 경사 하강법입니다.
경사하강법은 최적의 회귀식을 구하기 위해 사용되는 방법인데요.
선형 회귀의 경우 변수가 많으면 많을수록, 최소제곱법을 통해 최적의 계수(Coefficient)와 절편(Intercept)를 계산하기 시간이 오래 걸리게되는 등 많은 코스트가 발생하게 되는데요. 이를 해결하는 방법 중 하나가 경사하강법입니다.
1. 경사하강법(Gradient Descent)란?
- 경사하강법의 사전적인 의미는 '점진적인 하강' 입니다. 이 뜻에서 알 수 있듯이 점진적으로 반복적인 계산을 진행하여 비용함수의 w(Weight)를 최소화 시켜가는 것을 말합니다.
(여기서 w는, w0는 y 절편, w1,w2....wp는 xp의 계수를 의미합니다)
- 선형회귀 모델에서는 실제 값과 예측값의 차이(잔차 : Residual)를 최소화하는 회귀식을 찾으려고 하는데요.
- 잔차의 값은 양(+)의 값 또는 음(-)의 값일 수 있기에, 각 값의 절대크기를 포함한 식을 만들기 위해 아래와 같같은 '잔차 제곱 합'(Residual Sum of Squares) 이라는 식을 만들고 이를 최소화하는 절편(Intercept)와 계수(Coefficient)를 찾으면 됩니다.


이때, y_hat은 아래와 같이 표현됩니다.

- 즉, RSS를 최소화시키는 W 값들을 구해야하며, 이를 구하기 위해서는 각 w(w0, w1, ..... wp)에 대해서 편미분을 하여 0이 되는 식들을 찾아 연립계산해야되는 과정이 필요합니다.
- w의 개수가 많아지면(=p의 개수가 많아지면) 이 과정이 점차 복잡해지고 계산시간이 많이 소요됩니다. 또한, 추후에 다루겠지만 선형회귀가 아닌 더 복잡한 식에 대해서는 잔차를 최소화시키는 w 값을 찾기 위한 식이 더 복잡해지는데요.
- 이를 해결하기 위해 경사하강법(Gradient Descent)를 활용합니다. 경사하강법을 2차식으로 표현하면 아래와 같습니다.

* 최초 임의의 w를 선정하고
* 이후, 해당 지점에서 미분을 한 뒤
* 미분값에 반대 부호를 취하고 (ex. 미분값이 +1이면, -1)
* 위 부호에 여기에 일정 거리(Step)만큼을 곱해준 값을 최초 w에 더해줍니다.
ex) (최초 w) w -> (이후 w) w + (-1)x3 (step이 3인 경우)
- 이와 같은 방식으로 계속 업데이트 하다보면 위 그래프에서 표현되는 Global cost minimum, 즉 최소값에 도달한다는 의미입니다.
(위 그래프에서는, 앞서 설명한 방법을 통해 2차 그래프의 최소값이 미분값이 0이 되는 지점을 찾아간다는 것입니다)
2. 파이썬 코딩을 통해 알아보는 경사하강법
- 이번에는 파이썬 코딩을 통해 예제를 활용하여 경사하강법에 대해서 알아보겠습니다.
- 예제에서는 변수는 1개만 활용하여 2차원 그래프로 표현해보겠습니다.
* 먼저 예제 데이터를 만들어보겠습니다.
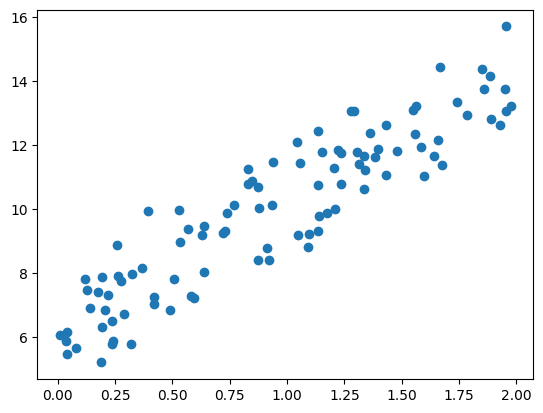
* numpy로 데이터를 만들고 pyplot으로 시각화해보았습니다. (y= 4x + 6 식에서 noise를 추가해서 데이터 생성)
|
1
2
3
4
5
6
7
8
9
10
11
|
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(0)
# y = 4X + 6 식을 근사(w1=4, w0=6). random 값은 Noise를 위해 만듬
X = 2 * np.random.rand(100,1)
y = 6 +4 * X+ np.random.randn(100,1)
# X, y 데이터 셋 scatter plot으로 시각화
plt.scatter(X, y)
|
cs |
* 이때, 해당 식은 2차 식이며 선형회귀가 도출하는 예측식은 아래와 같습니다.

* 여기서 잔차의 제곱합(RSS / Residual Sum of Squares)은 아래와 같이 정의됩니다.
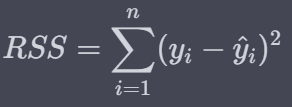

* 이제 w에 대해 각각 편미분(w0 : 절편, w1 : x의 계수)하게 되면 아래와 같은 결과가 나옵니다.
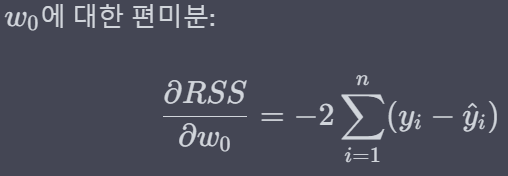
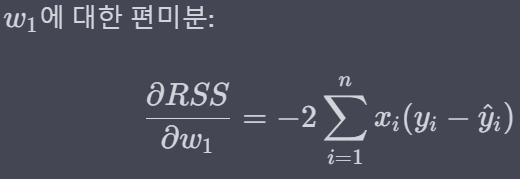
* 이제 위에서 도출된 편미분 값을 활용해 경사하강법을 진행해보겠습니다.
* 과정은
a) w0과 w1를 임의 값으로 설정하고 첫 비용 함수의 값을 계산
b-1) w1 업데이트 (new_w1로 명명) : w1에 학습률(위에서 언급한 일정크기를 말하며, 아래 예제에서는 0.01로 설정)과 w1에 대한 편미분값을 곱한 값을 더해줘서 업데이트
b-2) w0 업데이트 (new_w0로 명명) : w0에 학습률(위에서 언급한 일정크기를 말하며, 아래 예제에서는 0.01로 설정)과 w0에 대한 편미분값을 곱한 값을 더해줘서 업데이트
c) 이를 활용해 다시 비용함수 RSS를 계산
d) 비용 함수의 값이 업데이트 전의 (w0, w1) 값을 사용했을때보다 업데이트 후인 (new_w0, new_w1) 값을 사용했을때 더 감소하였다면 위 과정을 반복 / 감소하지 않았다면 중지
-> 더 감소하지않았다면 해당 지점이 RSS의 최소값이라고 가정하여 중단
와 같습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
# w1 과 w0 를 업데이트 할 w1_update, w0_update를 반환.
def get_weight_updates(w1, w0, X, y, learning_rate=0.01):
N = len(y)
# 먼저 w1_update, w0_update를 각각 w1, w0의 shape와 동일한 크기를 가진 0 값으로 초기화
w1_update = np.zeros_like(w1)
w0_update = np.zeros_like(w0)
# 예측 배열 계산하고 예측과 실제 값의 차이 계산
y_pred = np.dot(X, w1.T) + w0
diff = y-y_pred
# w0_update를 dot 행렬 연산으로 구하기 위해 모두 1값을 가진 행렬 생성
w0_factors = np.ones((N,1))
# w1과 w0을 업데이트할 w1_update와 w0_update 계산
w1_update = -(2/N)*learning_rate*(np.dot(X.T, diff))
w0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T, diff))
return w1_update, w0_update
|
cs |
* 위에서 함수를 정의했으니 이제 함수의 들어갈 최초값들과 일부 식들을 정의해줍니다.
|
1
2
3
4
5
6
7
8
9
10
|
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
y_pred = np.dot(X, w1.T) + w0
diff = y-y_pred
print(diff.shape)
w0_factors = np.ones((100,1))
w1_update = -(2/100)*0.01*(np.dot(X.T, diff))
w0_update = -(2/100)*0.01*(np.dot(w0_factors.T, diff))
print(w1_update.shape, w0_update.shape)
w1, w0
|
cs |
* 다음은 위에서 정의한 get_weight_updates() 함수를 경사 하강 방식으로 반복수행하여 w1과 w0을 업데이트하는 함수인 gradient_descent_steps()함수를 정의합니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
# 입력 인자 iters로 주어진 횟수만큼 반복적으로 w1과 w0를 업데이트 적용함.
def gradient_descent_steps(X, y, iters=10000):
# w0와 w1을 모두 0으로 초기화.
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
# 인자로 주어진 iters 만큼 반복적으로 get_weight_updates() 호출하여 w1, w0 업데이트 수행.
for ind in range(iters):
w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0
|
cs |
* 이제 gradient_descent_steps()를 호출해 w1과 w0를 구해보겠습니다. 그리고 최종적으로 예측값과 실제값의 RSS 차이를 계산하는 get_cost() 함수를 생성하고 이를 이용해 경사 하강법의 예측 오류도 계산해보겠습니다.
|
1
2
3
4
5
6
7
8
9
|
def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N
return cost
w1, w0 = gradient_descent_steps(X, y, iters=1000)
print("w1:{0:.3f} w0:{1:.3f}".format(w1[0,0], w0[0,0]))
y_pred = w1[0,0] * X + w0
print('Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))
|
cs |

최초 데이터가 y= 4x + 6 의 식에서 노이즈를 추가해서 나온 데이터들의 분포로 구성되었기에 위에서 구한 경사하강법의 결과 값인 w1 = 4.022 와 w0= 6.162는 꽤나 괜찮아보입니다.
* 위 결과를 시각화 해보면 아래와 같습니다.
|
1
2
|
plt.scatter(X, y)
plt.plot(X,y_pred)
|
cs |
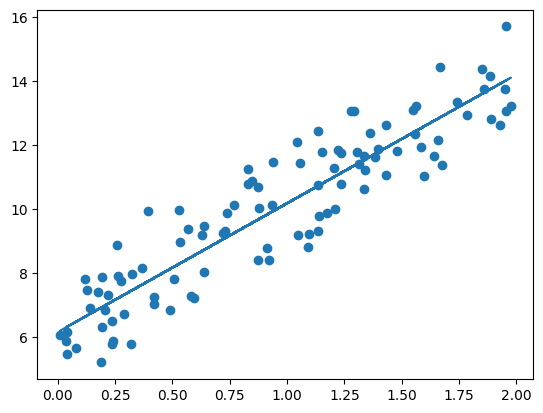
* 일반적으로 경사하강법은 모든 학습 데이터에 대해 반복적으로 비용함수 최소화를 위한 값을 업데이트 하기때문에 수행 시간이 매우 오래 걸린다는 단점이 있습니다. 이 때문에 사용하는 것이 확률적 경사 하강법 입니다.
3. 확률적 경사하강법(Stochastic Gradient Descent)
- 확률적 경사하강법은 전체 입력 데이터로 w가 업데이트되는 값을 계산하는 것이 아닌, 일부 데이터만 이요해 w가 업데이트되는 값을 계산하는 방법으로, 빠른 속도를 보장합니다.
- 이로 인해, 대용량의 데이터 경우 확률적 경사하강법 또는 미니 배치(mini batch) 확률적 경사하강법을 이용해 최적 비용함수르 도출합니다.
* 미니 배치(min-batch)란? 배치(batch)는 전체 데이터의 일부를 의미하며, 미니 배치는 전체 데이터의 작은 일부를 의미합니다.
* 이번에는 확률적 경사하강법을 함수로 정의해보겠습니다. 이때 배치의 크기는 10으로(전체 데이터 중 하나의 배치에 10개만 취한다는 의미)으로, 업데이트 반복회수는 1,000번으로 정의하였습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
def stochastic_gradient_descent_steps(X, y, batch_size=10, iters=1000):
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
prev_cost = 100000
iter_index =0
for ind in range(iters):
np.random.seed(ind)
# 전체 X, y 데이터에서 랜덤하게 batch_size만큼 데이터 추출하여 sample_X, sample_y로 저장
stochastic_random_index = np.random.permutation(X.shape[0])
sample_X = X[stochastic_random_index[0:batch_size]]
sample_y = y[stochastic_random_index[0:batch_size]]
# 랜덤하게 batch_size만큼 추출된 데이터 기반으로 w1_update, w0_update 계산 후 업데이트
w1_update, w0_update = get_weight_updates(w1, w0, sample_X, sample_y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0
|
cs |
* 위에서 정의된 식에 w1과 w0을 입력하고 결과를 도출하면 아래와 같습니다.
|
1
2
3
4
|
w1, w0 = stochastic_gradient_descent_steps(X, y, iters=1000)
print("w1:",round(w1[0,0],3),"w0:",round(w0[0,0],3))
y_pred = w1[0,0] * X + w0
print('Stochastic Gradient Descent Total Cost:{0:.4f}'.format(get_cost(y, y_pred)))
|
cs |

- 앞서 구한 w0, w1의 결과와 큰 차이가 없는 결과를 도출했습니다. 또한 예측 비용 오류는 0.9937로 0.9935였던 기존 결과보다 아주 조금 높을 뿐 큰 예측 성능상 차이가 없음을 알 수 있습니다.
- 이로 인해, 대용량의 데이터를 처리할 때는 확률적 경사 하강법을 많이 이용합니다.
'머신러닝 with Python' 카테고리의 다른 글
| [머신러닝 with 파이썬] 회귀 트리(Regression Tree) (0) | 2023.09.23 |
|---|---|
| [머신러닝 with 파이썬] 로지스틱 회귀(Logistic Regression) (0) | 2023.09.22 |
| [머신러닝 with Python] 선형회귀(Linear Regression) / 당뇨병(Diabetes) 데이터 활용 / EDA 시각화 포함 (0) | 2023.09.19 |
| [머신러닝 with Python] 선형회귀(Linear Regression) / 최소제곱법(Least Square Methods) (1) (0) | 2023.09.18 |
| [머신러닝 with Python] Light GBM 실습 / 신용카드 사기 검출 데이터(Credit Card Fraud) 활용(2) (0) | 2023.09.17 |




댓글