
이번에 알아볼 것은 분류(Classification) 모델의 대표격인
결정트리 / 결정나무 (Decision Tree)
입니다.
1. 결정트리 / 결정나무(Decision Tree)란?
- 결정트리(Decision Tree)는 머신러닝 알고리즘 중 직관적으로 이해하기 쉬운 알고리즘의 대표격입니다.
- 분류(Classification) 모델의 대표격이지만, 회귀(Regression) 모델로도 활용할 수 있습니다.
- 해당 모델은 스무고개와 같은 if/else 기반의 룰을 연계하여 데이터를 분류 (또는 회귀)를 합니다.
- 결정트리(Decision Tree)의 주요 특징은 아래와 같습니다.
1) 계층적 구조: 결정 나무는 계층적으로 구성된 트리 모양의 구조를 가지며, 맨 위에는 "루트 노드"가 있고, 이후에는 "분기 노드"와 "리프 노드"로 나뉩니다.
(* 노드 : 결정 트리에서의 "노드"는 결정 트리의 구조를 형성하며, 데이터의 특성 값을 기반으로 데이터를 분할하거나 예측을 수행하는 데 사용됩니다.)
2) 분할 규칙: 각 분기 노드는 입력 데이터의 특성을 기반으로 데이터를 두 개 이상의 하위 그룹으로 분할하는 규칙을 가지고 있습니다. 이 규칙은 데이터의 특성 값을 기준으로 적용됩니다.
3) 정보 이득(Information Gain) 또는 지니 불순도(Gini Impurity): 결정 나무는 각 분할에서 정보 이득이나 지니 불순도를 최대화하도록 분할 규칙을 선택합니다. 이러한 지표는 데이터 분할의 품질을 평가하는 데 사용됩니다.
4) 해석 가능성: 결정 나무는 해석하기 쉽고, 분류 또는 예측 결과를 해석할 수 있어 비전문가도 이해하기 쉽습니다.
5) 과적합(Overfitting) 관리: 결정 나무는 과적합을 관리하기 위한 몇 가지 기법을 사용할 수 있으며, 나무의 최대 깊이나 분기 노드의 최소 데이터 포인트 수를 제한하여 모델을 일반화할 수 있습니다.
2. 파이썬을 활용한 결정트리(Deicision Tree) 모델 만들기 + 시각화 (iris 데이터 활용)
- 이번에는 파이썬 코딩을 하면서 결정트리 모델을 만들어 보겠습니다.
- 모델 구축 간, 사용하게 될 데이터는 유명한 데이터인 iris 데이터인데요
* 붓꽃(iris) 데이터란?

붓꽃(iris) 데이터는 붓꽃의 품종(setosa / versicolor / virginica)에 따른 꽃잎(petal)의 길이 및 꽃받침(sepla)의 길이와 넓이가 정리된 데이터를 말합니다. 데이터의 일부분을 보면 아래와 같습니다.
|
1
2
3
4
5
6
7
8
9
|
import pandas as pd
from sklearn.datasets import load_iris
# Iris 데이터를 가져오기
iris_data = load_iris()
# 데이터프레임으로 변환
iris_df = pd.DataFrame(data=iris_data.data, columns=iris_data.feature_names)
iris_df.head()
|
cs |
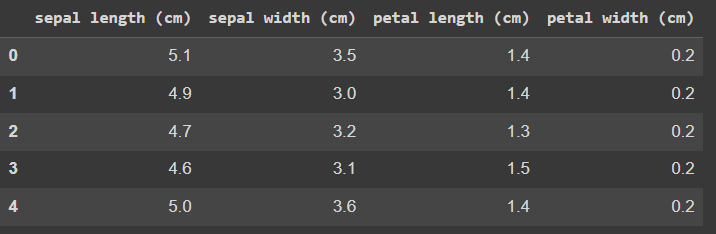
이제 iris 데이터를 바탕으로,
1) [모델생성] 결정트리를 만들고
2) [결과 시각화] 결정트리의 노드를 포함한 전체 구조를 Graphviz를 통해 시각화하며
3) [결과 해석] 각 변수들(features)이 분류 결과에 미치는 영향도를 Feature Importance를 활용해서 알아보겠습니다.
1) [모델생성] 결정트리 만들기
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import warnings
warnings.filterwarnings('ignore')
# DecisionTree Classifier 생성
dt_clf = DecisionTreeClassifier(random_state=156)
# 붓꽃 데이터를 로딩하고, 학습과 테스트 데이터 셋으로 분리
iris_data = load_iris()
X_train , X_test , y_train , y_test = train_test_split(iris_data.data, iris_data.target,
test_size=0.2, random_state=11)
# DecisionTreeClassifer 학습.
dt_clf.fit(X_train , y_train)
|
cs |
* 데이터는 사이킷런에 내장된 iris 데이터를 활용하며
* 해당 데이터를 학습(train)용과 테스트(test)용으로 분리한 뒤
* 분류용 결정트리 (DecisionTreeClassifier)를 만들어줍니다.
* 이때, 결정트리 구성간 조정해야될 하이퍼 파라미터는 기본값을 사용해줍니다.
(하이퍼 파라미터에 대해서는 다음에 자세히 알아보겠습니다.)
* 그리고, 결정트리 모델은 학습용 데이터 셋을 활용해 최초 학습모델을 만들어줍니다.
2) [결과 시각화] 결정트리의 노드를 포함한 전체 구조를 Graphviz를 통해 시각화
|
1
2
3
4
5
6
7
8
9
10
11
12
|
from sklearn.tree import export_graphviz
# export_graphviz()의 호출 결과로 out_file로 지정된 tree.dot 파일을 생성함.
export_graphviz(dt_clf, out_file="tree.dot", class_names=iris_data.target_names , \
feature_names = iris_data.feature_names, impurity=True, filled=True)
import graphviz
# 위에서 생성된 tree.dot 파일을 Graphviz 읽어서 Jupyter Notebook상에서 시각화
with open("tree.dot") as f:
dot_graph = f.read()
graphviz.Source(dot_graph)
|
cs |
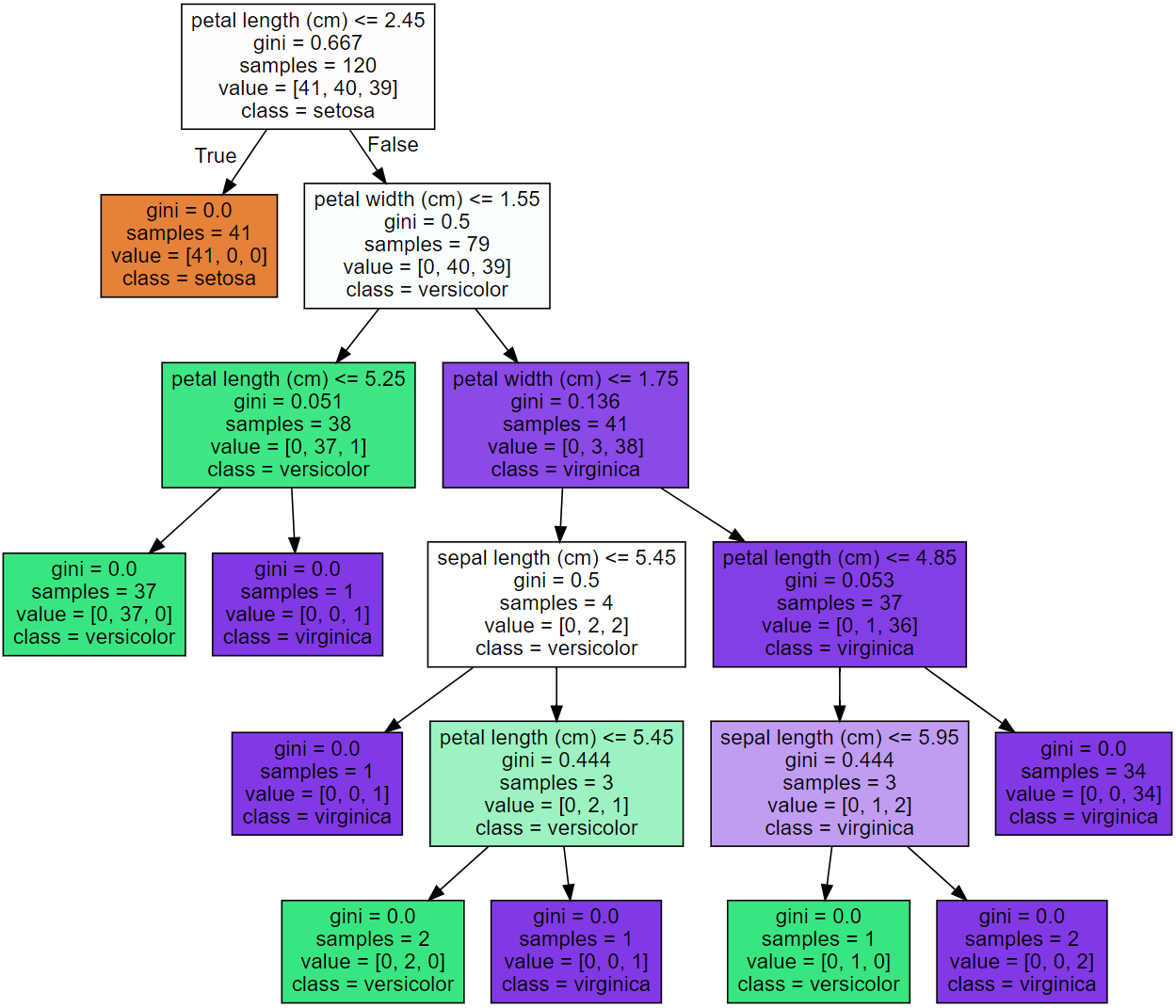
* Graphviz 라이브러리를 활용해서 학습된 모델이 어떤 알고리즘으로 분류했는지 그 결과를 시각화해줍니다.
* 첫번째 노드의 예시를 통해서 해석을 알아보면
a) "petal length가 2.45cm 보다 크냐 / 작냐" 에 따라 분류하며,
b) 이때 "크다"면 setosa로 분류한다는 의미입니다.
c) 이때 gini는 앞서 말씀드린 지니 불순도(Gini Impuriy)를 의미합니다.
c-1) 지니 불순도란, 분류 문제에서 노드(데이터 집합의 하위 그룹)의 불순도를 측정하는 지표를 말합니다.
이는, 노드에 속한 데이터 집합을 고려하고, 노드 내의 각 클래스(라벨)의 비율을 p(i)로 나타냅니다.
여기서 i는 클래스의 인덱스입니다.
이를 식으로 알아보면 아래와 같은데요

첫 번째 노드의 예시를 통해 해석해보면, value가 뜻하는 것은 각 붓꽃 품종의 개수를 뜻하며
이때 [41, 40, 39]는 setosa / versicolor / virginica 의 각 개수를 뜻합니다.
해당 데이터의 클래스 분포는 특정 클래스에 일관적이지 않은데요.
지니 불순도는 이러한 일관성이 떨어질수록(다양한 클래스가 여러 크기로 존재할수록) 낮은 값을 가집니다.
해당 집단의 지니 불순도를 위 식에 따라 계산해보면
Gini = 1 - { (41/120)^2 + (40/120)^2 + (39/120)^2 } = 0.667 이 나오게 됩니다.
만일, 데이터에 1개의 클래스만 존재한다면 Gini 계수는 0이 되며 지니 불순도가 0이라는 의미입니다.
(분류가 완벽하게 되었다는 의미)
* 이와 같은 방식으로 다음 노드들을 해석해나가시면 됩니다.
3) [결과 해석] 각 변수들(features)이 분류 결과에 미치는 영향도를 Feature Importance를 활용
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
import seaborn as sns
import numpy as np
%matplotlib inline
# feature importance 추출
print("Feature importances:\n{0}".format(np.round(dt_clf.feature_importances_, 3)))
# feature별 importance 매핑
for name, value in zip(iris_data.feature_names , dt_clf.feature_importances_):
print('{0} : {1:.3f}'.format(name, value))
# feature importance를 column 별로 시각화 하기
sns.barplot(x=dt_clf.feature_importances_ , y=iris_data.feature_names)
|
cs |
이번에는 각 변수들(sepal length/width, petal length/width)이 분류 결과(setosa 인가? versicolor 인가? virginica 인가?)에 어느정도의 영향을 미치는지 알아보겠습니다.
이에 대한 방법 중 Feature Importance를 활용하겠습니다.
* Feature Importance(특성 중요도)는 기계 학습 모델에서 사용된 특성(데이터의 열 또는 변수)이 모델의 예측에 얼마나 중요한 역할을 하는지를 평가하는 지표
* 결정 트리 기반 모델(Decision Tree, Random Forest, Gradient Boosting 등)의 특성 중요도
결정 트리 기반 모델은 노드를 분할할 때 특성 중요도를 고려하여 가장 중요한 특성을 상위 노드에 배치하여
해당 중요도를 계산합니다.
이는 노드 분할 시 지니 불순도(또는 엔트로피)의 감소 또는 분할 기준에 따라 계산되며
중요한 특성은 노드 분할에 큰 기여를 하는 특성이라 할 수 있습니다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
import seaborn as sns
import numpy as np
%matplotlib inline
# feature importance 추출
print("Feature importances:\n{0}".format(np.round(dt_clf.feature_importances_, 3)))
# feature별 importance 매핑
for name, value in zip(iris_data.feature_names , dt_clf.feature_importances_):
print('{0} : {1:.3f}'.format(name, value))
# feature importance를 column 별로 시각화 하기
sns.barplot(x=dt_clf.feature_importances_ , y=iris_data.feature_names)
|
cs |

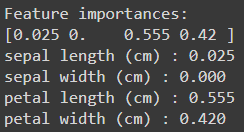
해당 모델의 학습 간 계산된 특성(Features, petal length/width 및 sepal length/width)들의 중요성을 계산해보면 위와 같습니다.
이를 해석해보면
* sepal width의 중요도는 0 / sepal length의 중요도는 0.025(=2.5%) / petal length의 중요도는 0.555(=55.5%) / petal width의 중요도는 0.420(=42%)입니다.
* 즉, petal length > petal width > sepal length 순으로 중요하며, sepal width는 분류 결과에 영향을 미치지 않는다는 결과를 도출했습니다.
물론, 이것만을 보고 직관적인 해석은 제한됩니다. 이를 해결하기 위한 XAI(eXplainable AI)의 방법 중 하나로 Shapley Value라는 것이 있는데 해당 내용은 다른 트리 기반의 모델들을 정리한 뒤 한번 정리해보겠습니다.




댓글