
[머신러닝 with Python] 상점 신용카드 매출 예측 (DACON 문제) (1/2)
지난번 포스팅에 이어지는 내용입니다.
이번에는 상점별 매출 특성을 분석해보겠습니다.
제공된 데이터에는 총 1,967개의 상점이 있으며, 시계열 그래프를 통해 데이터에 있는 상점들이 어떤 특성을 가지는지 파악해보겠습니다. 상점의 특징을 계절성이 있는 상점, 추세가 있는 상점, 휴업중인 상점 이렇게 3가지로 분류했습니다.
1) 계절성이 있는 상점
예측할 시기는 봄이고, 1학기, 상반기, 축제 등 다양한 계절성을 가지고 있습니다. 먼저 시각화를 통해 변환된 데이터를 출력해봅니다.
# 상점 아이디가 257번인 데이터를 시리즈 객체로 데이터 출력
store_257 = time_series(resampling_data, 257)
store_257
# 시계열 그래프 그리기
store_plot_257 = store_257.plot()
fig = store_plot_257.get_figure()
fig.set_size_inches(13.5,5)
위 그림에서 보듯 계절 별로 매출의 변동이 확연히 다른 형태를 띄는 업종이 있음을 알 수 있습니다.
2) 추세가 있는 상점
# 상점 아이디가 335번인 상점의 시계열 그래프
store_335 = time_series(resampling_data, 335)
store_plot_335 = store_335.plot()
fig = store_plot_335.get_figure()
fig.set_size_inches(13.5,5)
위 그림에서 보듯 계절적인 변동이 아닌, 좀 더 큰 시계열 범위에서의 추세가 보이는 형태의 상점도 있습니다.
3) 휴업중인 상점
# 상점 아이디가 111번인 데이터를 시리즈 객체로 데이터 출력
store_111 = time_series(resampling_data, 111)
store_111
# 상점 아이디가 111번인 상점의 시계열 그래프
store_plot_111 = store_111.plot()
fig = store_plot_111.get_figure()
fig.set_size_inches(13.5,5)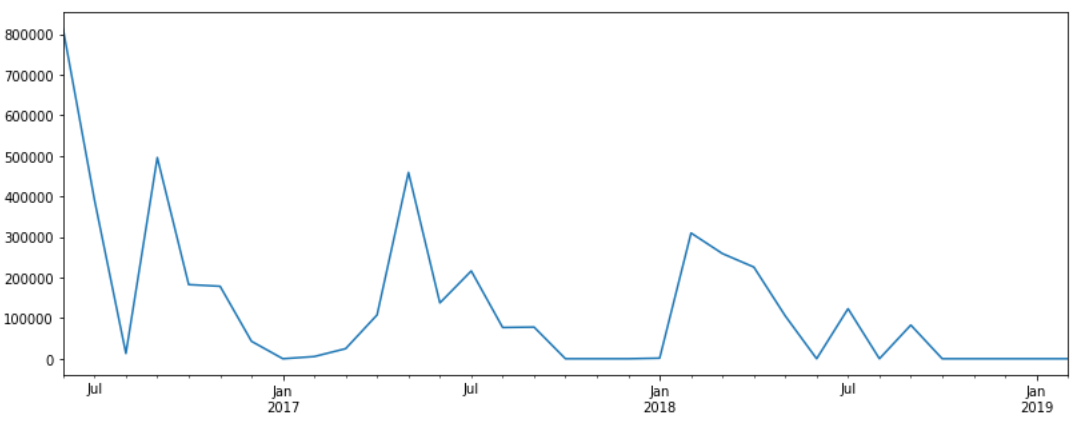
몇개월 동안 매출이 거의 나오지 않는 상점의 예시는 위와 같습니다.
이번에는 시계열 데이터의 정상성에 대해서 알아보겠습니다.
시계열 데이터의 정상성이란, 추세나 계절성이 없는 시계열 데이터를 의미합니다. 즉, 정상의 의미는 데이터가 시간의 변동에 따라 평균과 분산이 일정한다는 뜻입니다.
위 정의에 따르면 추세나 계절성이 있는 상점의 데이터는 정상성이 있는 시계열 데이터가 아닙니다.
이러한 시계열 데이터의 정상성을 판단하기 위해 ADF Test를 사용해보았습니다.
ADF - Test는 Augmented Dicky-Fuller Test의 약자로, 시계열 데이터가 정상을 가지는지를 판단할 때 사용하며, 회귀분석 결과로 나온 계수를 검정 통계량으로 사용합니다.
- ADF Test를 통해 시계열 데이터가 정상성을 가지는지 검정하고 정상성을 가지지 않으면 차분(Differencing)을 통해 평균을 일정하게 만들어줘야합니다.
* 차분(Differencing)은 비정상 시계열을 평균이 일정한 정상 시계열로 바꾸는 기법입니다.
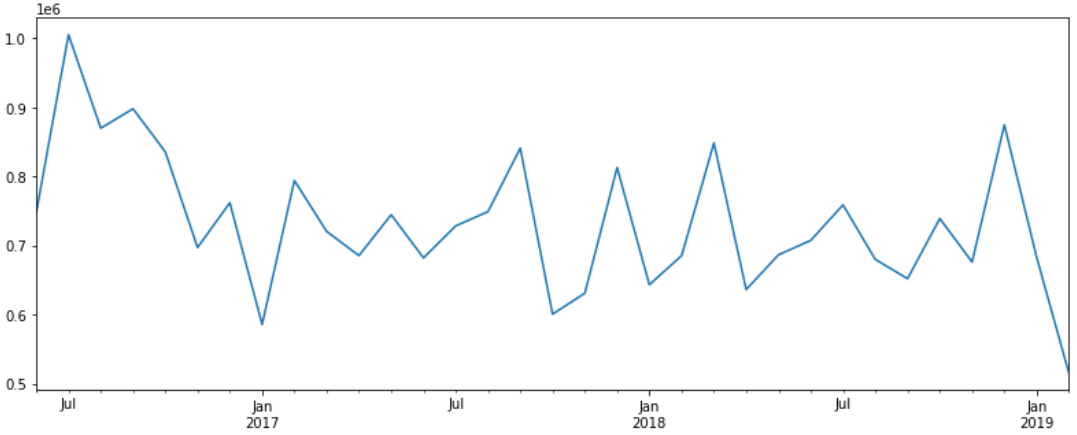
정상 시계열로 추정되는 0번 상점과 비정상 시계열로 추정되는 257번 상점의 시계열 그래프를 그려보겠습니다.
# 상점 아이디가 0번인 상점의 시계열 그래프
store_0 = time_series(resampling_data, 0)
store_plot_0 = store_0.plot()
fig = store_plot_0.get_figure()
fig.set_size_inches(13.5,5)
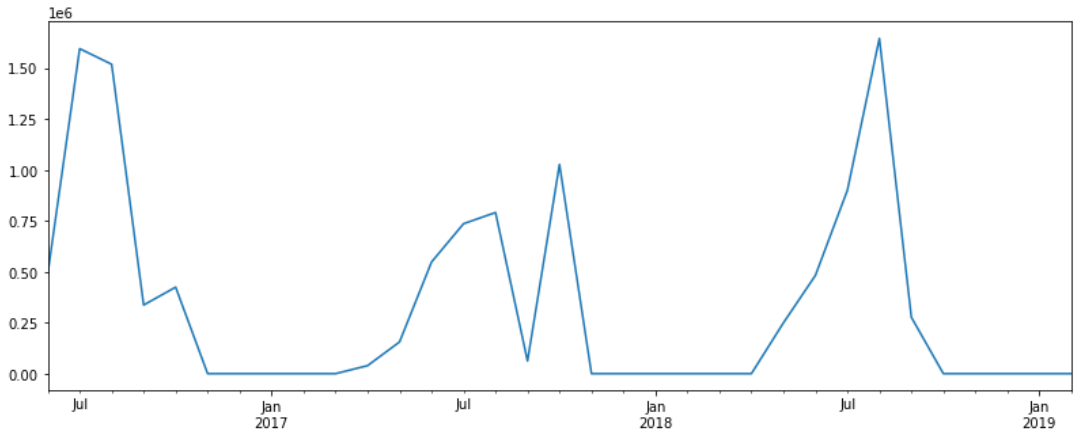
# 상점 아이디가 257번인 상점의 시계열 그래프
store_257 = time_series(resampling_data, 257)
store_plot_257 = store_257.plot()
fig = store_plot_257.get_figure()
fig.set_size_inches(13.5,5)
이제 ADF-Test를 통해 0번과 257번 상점이 정상 시계열인지 확인해보겠습니다.
(ADF Test간 귀무가설은 해당 시계열 자료가 정상 시계열이 아니다이고 대립 가설은 시계열 자료가 정상성을 만족한다 입니다.)
# pmdarima 패키지에 있는 ADFTest 클래스를 임포트
from pmdarima.arima import ADFTest
# 상점 아이디가 0번인 데이터를 시리즈 객체로 변환
store_0 = time_series(resampling_data, 0)
# ADF-Test 시행
p_val, should_diff = ADFTest().should_diff(store_0)
print('p_val : %f , should_diff : %s' %(p_val, should_diff))0번 데이터의 검정 결과, 아래와 같이 Differencing이 필요하지 않은 정상데이터임을 확인할 수 있습니다.

# 상점 아이디가 257번인 데이터를 시리즈 객체로 변환
store_257 = time_series(resampling_data, 257)
# ADF-Test 시행
p_val, should_diff = ADFTest().should_diff(store_257)
print('p_val : %f , should_diff : %s' %(p_val, should_diff))257번 데이터의 검정 결과, 아래와 같이 Differencing이 필요한 비정상 데이터임을 확인할 수 있습니다.
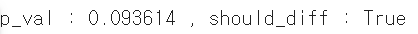
이제 모든 데이터에 대해서 ADF_Test를 진행해보겠습니다.
## ARIMA 모델의 차분 여부를 결정하기 위한 단위근 검정
def adf_test(y):
return ADFTest().should_diff(y)[0]
adf_p = []
count = 0
skipped = []
for i in tqdm(resampling_data['store_id'].unique()):
ts = time_series(resampling_data,i)
try:
p_val = adf_test(ts)
if p_val < 0.05:
count += 1
adf_p.append(p_val)
except:
skipped.append(i)
plt.figure(figsize=(8, 4))
sns.boxplot(adf_p)각 상점들의 p_value를 도출하여 이에 대한 분포를 box plot으로 확인해보니 대부분의 상점이 아래와 같이 기준점이 0.05보다 높은 것을 확인할 수 있습니다.

이제 시계열 모델윽 구축해보겠습니다. 이때 활용할 패키지는 R에서 활용되는 forecast 패키지 및 이에 연동되는 ARIMA, 지수평활법, 그리고 STL입니다.
먼저 forecast 패키지를 설치합니다.
from rpy2.robjects.packages import importr # rpy2 내의 패키지를 불러올 importr 클래스
utils = importr('utils') # utils 패키지를 임포트
utils.install_packages('forecast') # r의 forecast 패키지 설치.
utils.install_packages('forecastHybrid') # r의 forecastHybrid 패키지 설치
이후 auto_arima 함수를 활용해 모델으 생성하여 미래 3개월의 매출액을 예측해봅니다.
예시는 0번 상점입니다.
import rpy2.robjects as robjects # r 함수를 파이썬에서 사용 가능하게 변환하는 모듈
from rpy2.robjects import pandas2ri # 파이썬 자료형과 R 자료형의 호환을 도와주는 모듈
# pandas2ri를 활성화
pandas2ri.activate()
auto_arima = """
function(ts){
library(forecast) # forecast 패키지 로드
d_params = ndiffs(ts) # 시계열 자료의 차분 횟수 계산
model = auto.arima(ts, max.p=2, d=d_params) # auto.arima 모델 생성
forecasted_data = forecast(model, h=3) # 이후 3개월(h=3)을 예측
out_df = data.frame(forecasted_data$mean) # 예측값을 R의 데이터프레임으로 변환
colnames(out_df) = c('amount') # amount라는 열로 이름을 지정
out_df
}
"""
# r() 함수로 r 자료형을 파이썬에서 사용 가능
auto_arima = robjects.r(auto_arima)
ts = robjects.r('ts')# r 자료형 time series 자료형으로 만들어주는 함수
c = robjects.r('c') # r 자료형 벡터를 만들어주는 함수
store_0 = resampling_data[resampling_data['store_id']==0]
start_year = int(min(store_0['year_month'])[:4]) # 영업 시작 년도
start_month = int(min(store_0['year_month'])[5:]) # 영업 시작 월
# R의 ts 함수로 r의 time series 자료형으로 변환
train = ts(store_0['amount'], start=c(start_year, start_month), frequency=12)
#ensemble model
forecast = auto_arima(train)
np.sum(pandas2ri.ri2py(forecast).values) # 3개월 매출을 합산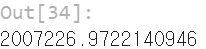
이제 ARIMA, 즉 자기회귀누적이동평균 모델에 대해서 알아보겠습니다.
ARIMA는 AR(Auto Regressive) 와 Integrated MA(Moving Average)가 합쳐진 것으로
자기회귀모델(AR, 과거의 데이터가 미래의 데이터에 영향을 미치는 모델)과 누적이동평균(IMA, 과거의 이동 평균들의 잔차가 미래의 데이터에 영향을 미치는 모델)을 합친 모델입니다.
이 모델은 시계열 데이터가 정상서인 경우에 주로 적용되며, 초기 차분 단계를 한번 이상 적용해 비정상성을 제거할 수 있습니다.
이제 이 모델을 활용해 전체 데이터에 대해 3개월 뒤의 매출액을 예측해보겠습니다.
import rpy2.robjects as robjects # r 함수를 파이썬에서 사용 가능하게 변환하는 모듈
from rpy2.robjects import pandas2ri # 파이썬 자료형과 R 자료형의 호환을 도와주는 모듈
# pandas2ri를 활성화
pandas2ri.activate()
auto_arima = """
function(ts){
library(forecast) # forecast 패키지 로드
d_params = ndiffs(ts) # 시계열 자료의 차분 횟수 계산
model = auto.arima(ts, max.p=2, d=d_params) # auto.arima 모델 생성
forecasted_data = forecast(model, h=3) # 이후 3개월(h=3)을 예측
out_df = data.frame(forecasted_data$mean) # 예측값을 R의 데이터프레임으로 변환
colnames(out_df) = c('amount') # amount라는 열로 이름을 지정
out_df
}
"""
# r() 함수로 r 자료형을 파이썬에서 사용 가능
auto_arima = robjects.r(auto_arima)# str 형식으로 정의된 auto_arima
ts = robjects.r('ts')# r 자료형 time series 자료형으로 만들어주는 함수
c = robjects.r('c') # r 자료형 벡터를 만들어주는 함수
final_pred = []
for i in tqdm(resampling_data.store_id.unique()):
store = resampling_data[resampling_data['store_id']==i]
start_year = int(min(store['year_month'])[:4]) ## 영업 시작 년도
start_month = int(min(store['year_month'])[5:]) ## 영업 시작 월
# R의 ts 함수로 time series 데이터로 변환
train = ts(store['amount'], start=c(start_year, start_month), frequency=12)
# 자동회귀누적이동평균 model
forecast = auto_arima(train)
# 3개월 매출을 합산, final_pred에 추가
final_pred.append(np.sum(pandas2ri.ri2py(forecast).values))
해당 결과를 submission 파일로 저장해주고 확인해봅니다.
submission = pd.read_csv('./submission.csv')
submission['amount'] = final_pred
submission.to_csv('submission.csv', index=False)
submission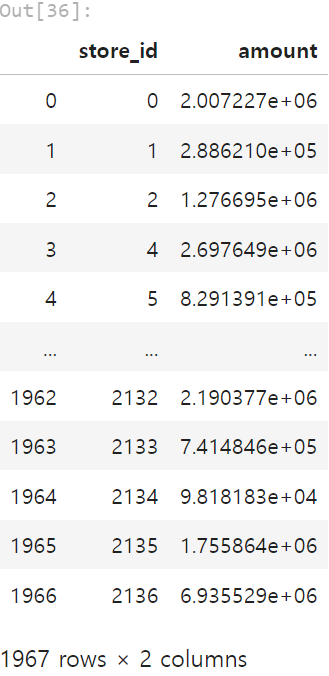
이렇게 나온 결과치만으로도 준수한 결과를 얻을 수 있지만
여기에 추가적으로 지수평활법을 적용해보겠습니다.
지수 평활법은 가장 최근 관측값을 가장 중요하게 생각하고 이전의 모든 관측값은 미래를 예측할 때 아무런 정보도 주지않는다고 가정하는 방법입니다.
import rpy2.robjects as robjects # r 함수를 파이썬에서 사용 가능하게 변환하는 모듈
from rpy2.robjects import pandas2ri # 파이썬 자료형과 R 자료형의 호환을 도와주는 모듈
# pandas2ri를 활성화
pandas2ri.activate()
ets = """
function(ts){
library(forecast) # forecast 패키지 로드
model = ets(ts) # AIC가 낮은 지수평활 모델을 찾음
forecasted_data = forecast(model, h=3) # 이후 3개월(h=3)을 예측
out_df = data.frame(forecasted_data$mean) # 예측값을 R의 데이터프레임으로 변환
colnames(out_df) = c('amount') # amount라는 열로 이름을 지정
out_df
}
"""
# r() 함수로 r 자료형을 파이썬에서 사용 가능
ets = robjects.r(ets)# str 형식으로 정의된 ets
ts = robjects.r('ts')# r 자료형 time series 자료형으로 만들어주는 함수
c = robjects.r('c') # r 자료형 벡터를 만들어주는 함수
final_pred = []
for i in tqdm(resampling_data.store_id.unique()):
store = resampling_data[resampling_data['store_id']==i]
start_year = int(min(store['year_month'])[:4]) # 영업 시작 년도
start_month = int(min(store['year_month'])[5:]) # 영업 시작 월
# R의 ts 함수로 time series 데이터로 변환
train = ts(store['amount'], start=c(start_year, start_month), frequency=12)
# 지수평활법l
forecast = ets(train)
# 3개월 매출을 합산, final_pred에 추가
final_pred.append(np.sum(pandas2ri.ri2py(forecast).values))
이번에 활용할 지수평활법은 시계열 데이터에 대해 AIC 값을 최소로 하는 지수평활 모델을 사용하고자 합니다. AIC는 주어진 데이터셋에서 통계 모델의 상대적 품질을 의미하는 것으로, AIC는 모델의 적합도가 높고 파라미터 개수가 작은 모델을 찾을 때 도움이 되는 지표입니다.
이를 활용한 결과입니다.
import rpy2.robjects as robjects # r 함수를 파이썬에서 사용 가능하게 변환하는 모듈
from rpy2.robjects import pandas2ri # 파이썬 자료형과 R 자료형의 호환을 도와주는 모듈
# pandas2ri를 활성화
pandas2ri.activate()
ets = """
function(ts){
library(forecast) # forecast 패키지 로드
model = ets(ts) # AIC가 낮은 지수평활 모델을 찾음
forecasted_data = forecast(model, h=3) # 이후 3개월(h=3)을 예측
out_df = data.frame(forecasted_data$mean) # 예측값을 R의 데이터프레임으로 변환
colnames(out_df) = c('amount') # amount라는 열로 이름을 지정
out_df
}
"""
# r() 함수로 r 자료형을 파이썬에서 사용 가능
ets = robjects.r(ets)# str 형식으로 정의된 ets
ts = robjects.r('ts')# r 자료형 time series 자료형으로 만들어주는 함수
c = robjects.r('c') # r 자료형 벡터를 만들어주는 함수
final_pred = []
for i in tqdm(resampling_data.store_id.unique()):
store = resampling_data[resampling_data['store_id']==i]
start_year = int(min(store['year_month'])[:4]) # 영업 시작 년도
start_month = int(min(store['year_month'])[5:]) # 영업 시작 월
# R의 ts 함수로 time series 데이터로 변환
train = ts(store['amount'], start=c(start_year, start_month), frequency=12)
# 지수평활법l
forecast = ets(train)
# 3개월 매출을 합산, final_pred에 추가
final_pred.append(np.sum(pandas2ri.ri2py(forecast).values))
submission = pd.read_csv('./submission.csv')
submission['amount'] = final_pred
submission.to_csv('submission.csv', index=False)
submission

제출 결과 해당 모델의 결과가 기존 단순 ARIMA 모델보다 더 좋은 결과를 만들게 되었습니다.
이번에는 STL을 적용해보겠습니다
STL은 Seasonal and Trend decomposition using Losses 의 약자입니다.
STL은 시계열 데이터가 가진 시간주기를 알고 있는 경우 시계열 데이터를 계절성과 추세, 나머지 성분으로 분해하여 분석하는 기법입니다.
0번 상점에 적용해보겠습니다. 이때 시간 주기는 1년인 12개월로 했습니다.
from statsmodels.tsa.seasonal import seasonal_decompose
import matplotlib.pyplot as plt
store_0 = time_series(resampling_data, 0)
# STL 분해
stl = seasonal_decompose(store_0.values, freq=12)
stl.plot()
plt.show()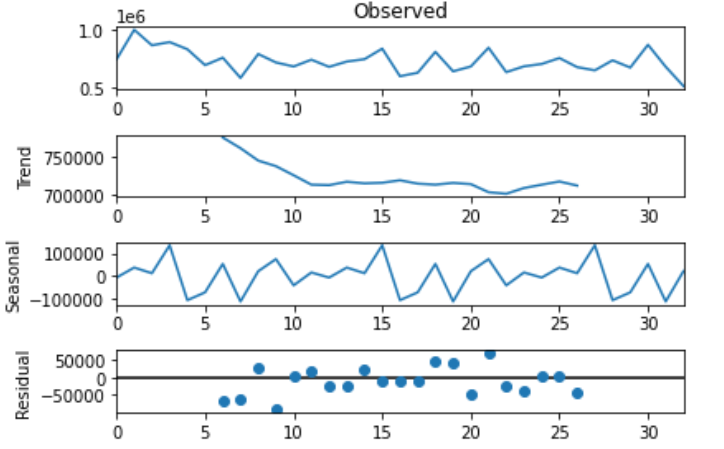
제일 위에있는 실제값(Observed) = Trend + Seosonal + Residual 로 구성됩니다. 이를 하는 이유는 매출의 전반적인 트렌드, 계절성 등을 고려해야 정확한 모델을 만들 수 있기 때문입니다.
이제 모든 데이터에 대해서 STL 분해후, 지수평활법을 통해 예측해보겠습니다.
기본적으로 STL 분해를 위해서는 최소 2시즌(24개월)보다 많은 데이터를 요구하기에 해당 내용을 적용하였습니다.
import rpy2.robjects as robjects # r 함수를 파이썬에서 사용 가능하게 변환하는 모듈
from rpy2.robjects import pandas2ri # 파이썬 자료형과 R 자료형의 호환을 도와주는 모듈
# pandas2ri를 활성화
pandas2ri.activate()
stlm = """
function(ts){
library(forecast) # forecast 패키지 로드
model = stlm(ts, s.window="periodic", method='ets') # STL 분해 후 지수평활법을 통한 예측
forecasted_data = forecast(model, h=3) # 이후 3개월(h=3)을 예측
out_df = data.frame(forecasted_data$mean) # 예측값을 R의 데이터프레임으로 변환
colnames(out_df) = c('amount') # amount라는 열로 이름을 지정
out_df
}
"""
ets = """
function(ts){
library(forecast) # forecast 패키지 로드
model = ets(ts) # AIC가 낮은 지수평활 모델을 찾음
forecasted_data = forecast(model, h=3) # 이후 3개월(h=3)을 예측
out_df = data.frame(forecasted_data$mean) # 예측값을 R의 데이터프레임으로 변환
colnames(out_df) = c('amount') # amount라는 열로 이름을 지정
out_df
}
"""
# r() 함수로 r을 파이썬에서 사용 가능
stlm = robjects.r(stlm)# str 형식으로 정의된 stlm
ets = robjects.r(ets)# str 형식으로 정의된 ets
ts = robjects.r('ts')# r 자료형 time series 자료형으로 만들어주는 함수
c = robjects.r('c') # r 자료형 벡터를 만들어주는 함수
final_pred = []
for i in tqdm(resampling_data.store_id.unique()):
store = resampling_data[resampling_data['store_id']==i]
data_len = len(store)
start_year = int(min(store['year_month'])[:4]) # 영업 시작 년도
start_month = int(min(store['year_month'])[5:]) # 영업 시작 월
# R의 ts 함수로 time series 데이터로 변환
train = ts(store['amount'], start=c(start_year, start_month), frequency=12)
# STL 분해를 적용한 지수평활 model
if data_len > 24:
forecast = stlm(train)
# 지수평활 model
else:
forecast = ets(train) # 3개월 매출을 합산, final_pred에 추가
final_pred.append(np.sum(pandas2ri.ri2py(forecast).values))
submission = pd.read_csv('./submission.csv')
submission['amount'] = final_pred
submission.to_csv('submission.csv', index=False)
submission
해당 결과를 submission 했을때 지수평활법 + AIC를 활용한 것보다 낮은 결과를 보여주었습니다.
이번에는 시계열 데이터의 변동 범위를 안정화시키기 위해 로그 변환의 효과를 확인해보겠습니다. 로그 변환을 통해 무조건 결과가 좋아지는 것은 아니기에 AUTO ARIMA 모델에 원본 결과와 변환된 결과를 각각 넣어서 그 결과를 비교해보겠습니다.
import rpy2.robjects as robjects # r 함수를 파이썬에서 사용 가능하게 변환하는 모듈
from rpy2.robjects import pandas2ri # 파이썬 자료형과 R 자료형의 호환을 도와주는 모듈
import numpy as np
# pandas2ri를 활성화
pandas2ri.activate()
auto_arima = """
function(ts){
library(forecast) # forecast 패키지 로드
d_params = ndiffs(ts) # 시계열 자료의 차분 횟수 계산
model = auto.arima(ts, max.p=2, d=d_params) # auto.arima 모델 생성
forecasted_data = forecast(model, h=3) # 이후 3개월(h=3)을 예측
out_df = data.frame(forecasted_data$mean) # 예측값을 R의 데이터프레임으로 변환
colnames(out_df) = c('amount') # amount라는 열로 이름을 지정
out_df
}
"""
# r() 함수로 r 자료형을 파이썬에서 사용 가능
auto_arima = robjects.r(auto_arima)
ts = robjects.r('ts')# r 자료형 time series 자료형으로 만들어주는 함수
c = robjects.r('c') # r 자료형 벡터를 만들어주는 함수
log = robjects.r('log')# 로그 변환 함수
exp = robjects.r('exp')# 로그 역변환 함수
# 0번 상점 추출
store_0 = resampling_data[resampling_data['store_id']==0]
start_year = int(min(store_0['year_month'])[:4]) # 영업 시작 년도
start_month = int(min(store_0['year_month'])[5:]) # 영업 시작 월
# train, test 분리
train = store_0[store_0.index <= len(store_0)-4]
test = store_0[store_0.index > len(store_0)-4]
# R의 ts 함수로 r의 time series 자료형으로 변환
train_log = ts(log(train['amount']), start=c(start_year, start_month), frequency=12) # log 정규화
train = ts(train['amount'], start=c(start_year, start_month), frequency=12) # log 정규화를 하지 않음
# model arima
forecast_log = auto_arima(train_log)
forecast = auto_arima(train)
# pred
pred_log = np.sum(pandas2ri.ri2py(exp(forecast_log)).values) #로그 역변환 후 3개월 합산
pred = np.sum(pandas2ri.ri2py(forecast).values) #3개월 매출을 합산
# test(2018-12~2019-02)
test = np.sum(test['amount'])
# mae
print('log-regularization mae: ', abs(test-pred_log))
print('mae:', abs(test-pred))
로그 변환이 더 유리함을 확인할 수 있습니다.
또한 여러 실험을 한 결과 변동계수(표준편차를 평균으로 나눈 지표)가 높은 상점의 경우에는 로그 정규화를 했을때 예측성능이 저하되는 것을 발견하여 매출액의 변동개수가 0.3미만인 상점만 로그 정규화를 진행후, 가장 성능이 좋았던 지수평활법을 이용해 예측해보겠습니다.
# 매출 변동 계수를 구하는 함수
def coefficient_variation(df, i):
cv_data = df.groupby(['store_id']).amount.std()/df.groupby(['store_id']).amount.mean()
cv = cv_data[i]
return cvimport rpy2.robjects as robjects # r 함수를 파이썬에서 사용 가능하게 변환하는 모듈
from rpy2.robjects import pandas2ri # 파이썬 자료형과 R 자료형의 호환을 도와주는 모듈
import numpy as np
# pandas2ri를 활성화
pandas2ri.activate()
ets = """
function(ts){
library(forecast) # forecast 패키지 로드
model = ets(ts) # AIC가 낮은 지수평활 모델을 찾음
forecasted_data = forecast(model, h=3) # 이후 3개월(h=3)을 예측
out_df = data.frame(forecasted_data$mean) # 예측값을 R의 데이터프레임으로 변환
colnames(out_df) = c('amount') # amount라는 열로 이름을 지정
out_df
}
"""
# r() 함수로 r 자료형을 파이썬에서 사용 가능
ets = robjects.r(ets)
ts = robjects.r('ts') # r 자료형 time series 자료형으로 만들어주는 함수
c = robjects.r('c') # r 자료형 벡터를 만들어주는 함수
log = robjects.r('log') # 로그 변환 함수
exp = robjects.r('exp')# 로그 역변환 함수
final_pred = []
for i in tqdm(resampling_data.store_id.unique()):
store = resampling_data[resampling_data['store_id']==i]
start_year = int(min(store['year_month'])[:4]) # 영업 시작 년도
start_month = int(min(store['year_month'])[5:]) # 영업 시작 월
cv = coefficient_variation(resampling_data, i)
# 매출액 변동 계수가 0.3 미만인 경우만 log를 씌움
if cv < 0.3:
train_log = ts(log(store['amount']), start=c(start_year,start_month), frequency=12)
# ets model
forecast_log = ets(train_log)
final_pred.append(np.sum(pandas2ri.ri2py(exp(forecast_log)).values))
# 매출액 변동 계수가 0.3 이상인 경우
else:
train = ts(store['amount'], start=c(start_year,start_month), frequency=12)
# 지수평활법
forecast = ets(train)
final_pred.append(np.sum(pandas2ri.ri2py(forecast).values))
이렇게 하니 기존 결과물들보다 조금은 향상된 점수를 기록할 수 있었습니다.
최종적으로는 지금까지 사용한 방법들을 앙상블해보겠습니다.
이를 원활하게 하기위해서 forecastHybrid 앙상블 기법을 활용합니다.
앙상블에 활용할 모델은 첫번째 사용한 자기회귀누적이동평균(ARIMA)와 두번째 활용한 지수평활법, 그리고 세번째로 알아본 STL 분해를 적용한 지수평활법입니다.
앙상블 하는 기준은 각 예측값을 평균하는 것입니다. 이때 aes는 ARIMA, ETS, STLM의 첫 앞글자를 딴 것을 의마합니다. 또한 앞서 알아보았던 것처럼 변동계수가 0.3미만일 경우에만 log 정규화를 진행해줍니다.
import rpy2.robjects as robjects # r 함수를 파이썬에서 사용 가능하게 변환하는 모듈
from rpy2.robjects import pandas2ri # 파이썬 자료형과 R 자료형의 호환을 도와주는 모듈
import numpy as np
# pandas2ri를 활성화
pandas2ri.activate()
hybridModel = """
function(ts){
library(forecast)
library(forecastHybrid)
d_params=ndiffs(ts)
hb_mdl<-hybridModel(ts, models="aes", # auto_arima, ets, stlm
a.arg=list(max.p=2, d=d_params), # auto_arima parameter
weight="equal") # 가중치를 동일하게 줌(평균)
forecasted_data<-forecast(hb_mdl, h=3) # 이후 3개월(h=3)을 예측
outdf<-data.frame(forecasted_data$mean)
colnames(outdf)<-c('amount')
outdf
}
"""
# r() 함수로 r 자료형을 파이썬에서 사용 가능
hybridModel = robjects.r(hybridModel)
ts = robjects.r('ts') # r 자료형 time series 자료형으로 만들어주는 함수
c = robjects.r('c') # r 자료형 벡터를 만들어주는 함수
log = robjects.r('log') # 로그 변환 함수
exp = robjects.r('exp')# 로그 역변환 함수
final_pred = []
for i in tqdm(resampling_data.store_id.unique()):
store = resampling_data[resampling_data['store_id']==i]
start_year = int(min(store['year_month'])[:4]) # 영업 시작 년도
start_month = int(min(store['year_month'])[5:]) # 영업 시작 월
cv = coefficient_variation(resampling_data, i)
# 매출액 변동 계수가 0.3 미만인 경우만 log를 씌움
if cv < 0.3:
train_log = ts(log(store['amount']), start=c(start_year,start_month), frequency=12)
# 앙상블 예측
forecast_log = hybridModel(train_log)
final_pred.append(np.sum(pandas2ri.ri2py(exp(forecast_log)).values))
# 매출액 변동 계수가 0.3 이상인 경우
else:
train = ts(store['amount'], start=c(start_year,start_month), frequency=12)
# 앙상블 예측
forecast = hybridModel(train)
final_pred.append(np.sum(pandas2ri.ri2py(forecast).values))
이렇게 앙상블하여 적용해주었더니 기존보다 훨씬 더 좋은 결과를 낼 수 있었습니다.
'머신러닝 with Python' 카테고리의 다른 글
| [머신러닝 with Python] 불균형 데이터 처리(1) : Credit Card Fraud Detection Data에 대해 EDA (1) | 2024.11.20 |
|---|---|
| [머신러닝 with Python] t-SNE란? (차원축소, 시각화) (0) | 2024.07.08 |
| [머신러닝 with Python] 상점 신용카드 매출 예측 (DACON 문제) (1/2) (0) | 2024.06.10 |
| [Machine Learning] What is machine learning? What is ML? (0) | 2024.03.06 |
| [머신러닝 with 파이썬] 군집화(클러스터링) : K-means & HDBSCAN / 시각화 (0) | 2023.09.27 |




댓글