
이번에 알아볼 내용은 차원축소를 통해 고차원의 데이터의 시각화를 할때 많이 사용하는 t-SNE 입니다.
1. t-SNE란?
- t-SNE는 t-distributed Stochastic Neighbor Embedding의 약자로, 고차원 데이터를 저차원 공간으로 시각화하기 위해 사용되는 비선형 차원축소 기법입니다.
- 이는 데이터의 클러스터링이나 구조적 관계를 시각적으로 이해하는데 유용한 방법입니다.
- t-SNE의 주요 작동 원리는 다음과 같습니다.
1) 고차원 데이터에서의 유사성 계산
* 고차원 공간에서 데이터 포인트 간의 유사성은 아래와 같은 조건부 확률 로 표현되며, 이는 데이터 포인트i 가 데이터 포인트 j를 선택할 확률을 의미합니다. (이 확률은 가우시안 분포를 기반으로 계산됩니다)

* 이때 포인트 i 의 분산은 각 포인트에 대해 개별적으로 설정되며, 주어진 Perplexity 값에 맞춰 조정됩니다.
(Perplexity : 각 포인트 주변의 유효한 이웃 수를 결정하는 하이퍼파라미터)
* 이때 전체확률인 Pij는 다음과 같습니다.(N = 전체 데이터 포인트의 수)

2) 저차원 데이터에서의 유사성 계산
* 저차원 공간에서는 t-분포를 사용하여 유사성을 모델링합니다. t-분포는 가우시안 분포보다 긴 꼬리(두꺼운 꼬리부분)을 가지므로, 저차원 공간에서 보다 잘 분리된 클러스터를 형성할 수 있습니다.
* 아래 그림은 가우시안 분포와 t 분포의 차이를 보여주는 그래프이며, degree of freedom이 커질수록 점차 꼬리쪽이 두꺼운 t 분포의 모습이 가우시안 분포의 모습을 따라감을 확인할 수 있습니다.

* 저차원에서의 유사성은 다음과 같이 계산됩니다.

이때, yi와 yj는 저차원 공간에서의 데이터 포인트 i와 j의 좌표를 의미합니다.
그림으로 이해해보면 아래와 같은데요.
* 왼쪽에 있는 그래프는 고차원 데이터이며, 각 점들끼리의 가우시안 분포 유사도는 아래와 Similarity Matrix에 있습니다.
* 오른쪽에 있는 그래프는 저차원 데이터이며, 각 점들끼리의 t-분포의 유사도는 아래 Similarity Matrix에 있습니다.
* t-SNE는 고차원 데이터의 gaussian similarity matrix와 가장 유사한 t-distribution similarity matrix를 만들어가는 것입니다.

3) KL Divergence 최소화
* 고차원 공간과 저차원 공간의 유사성 확률 분포 사이의 차이를 최소화히기 위해 Kullback-Leibler(KL) Divergence를 사용합니다.
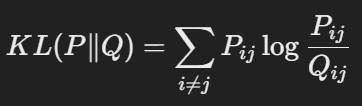
* 위 공식의 결과값이 최소가 되도록 하는 저차원 분포인 Qij를 찾아가는 것입니다.
4) 확률적 경사 하강법(SGD) 최적화
* KL 발산을 최소화기 위해 확률적 경사 하강법(Stochastic Gradient Descent, SGD)을 사용하여 저차원 좌표인 y들을 반복적으로 업데이트하고 각 반복마다 KL Divergence를 계산하고 이를 최소화하는 방향으로 업데이트 해나갑니다.
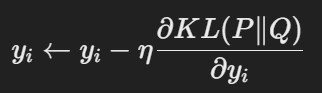
이를 통해 고차원 데이터는 시각화를 위해 2차원 또는 3차원으로 축소됩니다.
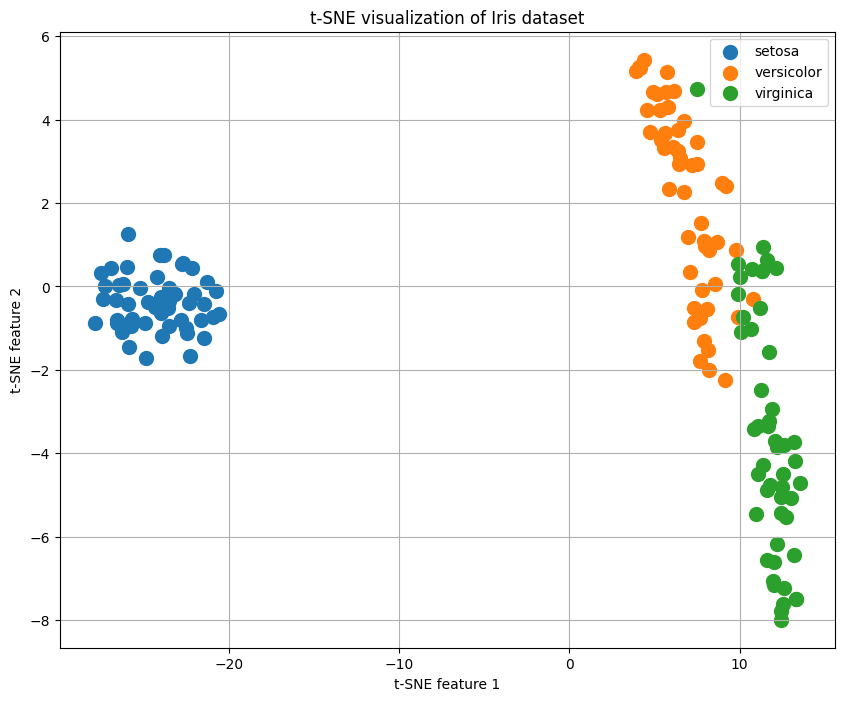
iris 데이터를 활용해 시각화 해보면 아래와 같습니다.
(2차원)
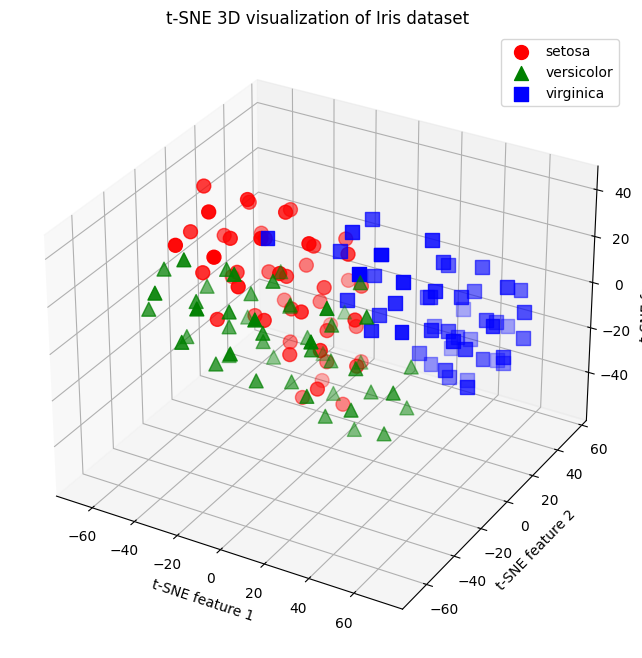
(3차원)
'머신러닝 with Python' 카테고리의 다른 글
| [머신러닝 with Python] 불균형 데이터 처리(2) : 불균형 클래스 분류 문제 평가지표 (0) | 2024.11.21 |
|---|---|
| [머신러닝 with Python] 불균형 데이터 처리(1) : Credit Card Fraud Detection Data에 대해 EDA (1) | 2024.11.20 |
| [머신러닝 with Python] 상점 신용카드 매출 예측 (DACON 문제) (2/2) (0) | 2024.06.11 |
| [머신러닝 with Python] 상점 신용카드 매출 예측 (DACON 문제) (1/2) (0) | 2024.06.10 |
| [Machine Learning] What is machine learning? What is ML? (0) | 2024.03.06 |




댓글